# Electromagnetism in Free Space
## 1 Introduction
### 1.1 Notation
**Definition 1.1.1 ** The **Cartesian coordinates system** is a coordinates system that uses three coordinates $(x,y,z)$ to define a point in three dimensional space. A position vector $\vec{r}$ can be written in terms of the elementary basis vectors $\hat{x},\hat{y},\hat{z}$,
\[\vec{r}=(x,y,z)=x \hat{x} + y \hat{y} + z \hat{z}\]
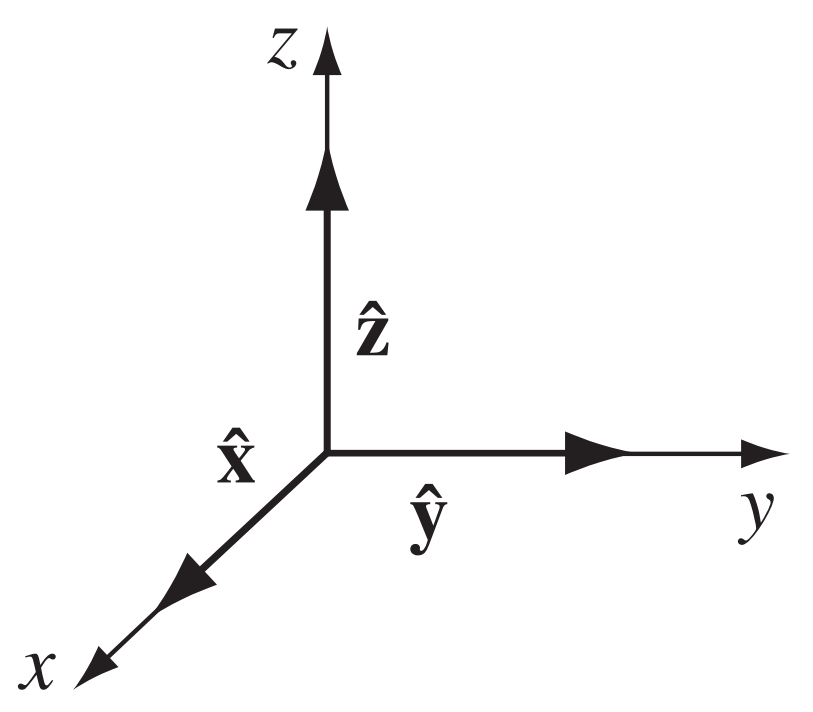 **File 1.1.1 ** Cartesian.png
**Definition 1.1.2 ** The **spherical coordinate system** is a coordinate system that uses three coordinates $(r,\theta,\phi)$ to define a point in three dimensional space. For a particular position we also define the basis vectors $\hat{r},\hat{\theta},\hat{\phi}$,
**File 1.1.1 ** Cartesian.png
**Definition 1.1.2 ** The **spherical coordinate system** is a coordinate system that uses three coordinates $(r,\theta,\phi)$ to define a point in three dimensional space. For a particular position we also define the basis vectors $\hat{r},\hat{\theta},\hat{\phi}$,
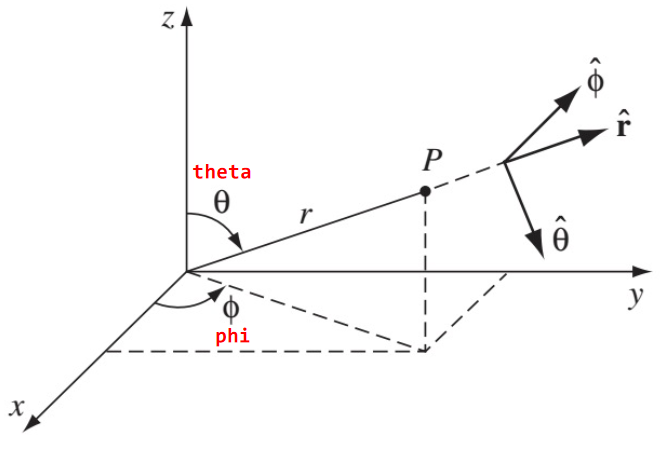 | | |
|:----------|:-------------|
| $r = \sqrt{x^2+y^2+z^2}\quad$ | $\hat{r} = \sin(\theta)\cos(\phi)\hat{x} + \sin(\theta)\sin(\phi)\hat{y}+\cos(\theta)\hat{z}$ |
| $\theta = \tan^{-1}(\sqrt{x^2+y^2}/2)\quad$ | $\hat{\theta}=\cos(\theta)\cos(\phi)\hat{x}+\cos(\theta)\sin(\phi)\hat{y}-\sin(\theta)\hat{z}$ |
| $\phi = \tan^{-1}(y/x)\quad$ | $\hat{\phi}=-\sin(\phi)\hat{x}+\cos(\phi)\hat{y}$ |
| $\ $ | $\ $ |
| $x = r\sin\theta\cos\phi\quad$ | $\hat{x} = \sin(\theta)\cos(\phi)\hat{r} + \cos(\theta)\cos(\phi)\hat{\theta} - \sin(\phi)\hat{\phi}$ |
| $y = r\sin\theta\sin\phi\quad$ | $\hat{y} = \sin(\theta)\sin(\phi)\hat{r} + \cos(\theta)\sin(\phi)\hat{\theta} + \cos(\phi)\hat{\phi}$ |
| $z = r\cos\theta\quad$ | $\hat{z} = \cos(\theta)\hat{r} - \sin(\theta)\hat{\theta}$ |
**File 1.1.2 ** Spherical.PNG
**Definition 1.1.3 ** The **cylindrical coordinate system** is a coordinate system that uses the three coordinates $(s,\phi,z)$ to define a point in three dimensional space. For a particular position we also define the basis vectors $\hat{s},\hat{\phi},\hat{z}$,
| | |
|:----------|:-------------|
| $r = \sqrt{x^2+y^2+z^2}\quad$ | $\hat{r} = \sin(\theta)\cos(\phi)\hat{x} + \sin(\theta)\sin(\phi)\hat{y}+\cos(\theta)\hat{z}$ |
| $\theta = \tan^{-1}(\sqrt{x^2+y^2}/2)\quad$ | $\hat{\theta}=\cos(\theta)\cos(\phi)\hat{x}+\cos(\theta)\sin(\phi)\hat{y}-\sin(\theta)\hat{z}$ |
| $\phi = \tan^{-1}(y/x)\quad$ | $\hat{\phi}=-\sin(\phi)\hat{x}+\cos(\phi)\hat{y}$ |
| $\ $ | $\ $ |
| $x = r\sin\theta\cos\phi\quad$ | $\hat{x} = \sin(\theta)\cos(\phi)\hat{r} + \cos(\theta)\cos(\phi)\hat{\theta} - \sin(\phi)\hat{\phi}$ |
| $y = r\sin\theta\sin\phi\quad$ | $\hat{y} = \sin(\theta)\sin(\phi)\hat{r} + \cos(\theta)\sin(\phi)\hat{\theta} + \cos(\phi)\hat{\phi}$ |
| $z = r\cos\theta\quad$ | $\hat{z} = \cos(\theta)\hat{r} - \sin(\theta)\hat{\theta}$ |
**File 1.1.2 ** Spherical.PNG
**Definition 1.1.3 ** The **cylindrical coordinate system** is a coordinate system that uses the three coordinates $(s,\phi,z)$ to define a point in three dimensional space. For a particular position we also define the basis vectors $\hat{s},\hat{\phi},\hat{z}$,
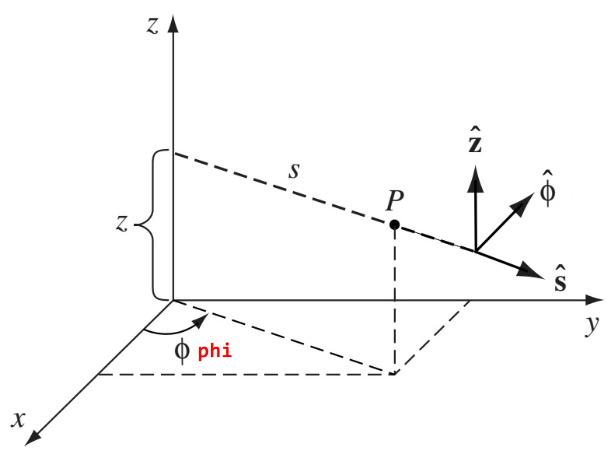 | | |
|:--|:--|
| $s = \sqrt{x^2+y^2}\quad$ | $\hat{s} = \cos(\phi)\hat{x} + \sin(\phi)\hat{y}$ |
| $\phi = \tan^{-1}(y/x)\quad$ | $\hat{\phi} = -\sin(\phi)\hat{x} + \cos(\phi)\hat{y}$ |
| $z=z\quad$ | $\hat{z}=\hat{z}$ |
| $\ $ | $\ $ |
| $x = s\cos\phi\quad$ | $\hat{x} = \cos(\phi)\hat{s} - \sin(\phi)\hat{\phi}$ |
| $y = s\sin\phi\quad$ | $\hat{y} = \sin(\phi)\hat{s} + \cos(\phi)\hat{\phi}$ |
| $z=z\quad$ | $\hat{z}=\hat{z}$ |
**File 1.1.3 ** Cylindrical.PNG
**Definition 1.1.4 ** The **Kronecker delta** $\delta_{ij} = \left\{\begin{array}{lr}
1, & \text{if } i = j\\
0, & \text{if } i\neq j
\end{array}\right\}$.
**Definition 1.1.5 ** The **Levi-Civita symbol** $\varepsilon_{a_1,a_2,\dots,a_n} = \left\{\begin{array}{rl}
+1, & \text{if } (a_1,a_2,\dots,a_n)\text{ is an even permutation of }(1,2,\dots,n)\\
-1, & \text{if } (a_1,a_2,\dots,a_n)\text{ is an odd permutation of }(1,2,\dots,n)\\
0, & \text{otherwise}
\end{array}\right\}$
**Definition 1.1.6 ** The **dot product** denoted $\vec{a}\cdot\vec{b}$ of two vectors $\vec{a}$ and $\vec{b}$ is the sum of the products of there components in any orthonormal basis.
\[\vec{a}\cdot\vec{b} = \sum_{i}a_ib_i\]
**Definition 1.1.7 ** The **cross product** of two vectors $\vec{a}$ and $\vec{b}$ is defined by the following sums of the products of there components in any orthonormal basis $\vec{e_1},\vec{e_2},\dots,\vec{e_n}$.
\[\vec{a}\times\vec{b} = \sum_i\sum_j\sum_k\varepsilon_{ijk}a_jb_k \vec{e_i}\]
**Definition 1.1.8 ** The **gradient** denoted $\nabla F$ of a differentiable scalar field $F$ is the vector field defined by the partial derivatives of the scalar field.
\[\nabla F = \frac{\partial F}{\partial x}\hat{x} + \frac{\partial F}{\partial y}\hat{y} + \frac{\partial F}{\partial z}\hat{z}=\left(\frac{\partial F}{\partial x},\frac{\partial F}{\partial y},\frac{\partial F}{\partial z}\right)\]\[\nabla F = \frac{\partial F}{\partial r}\hat{r} + \frac{1}{r}\frac{\partial F}{\partial \theta}\hat{\theta} + \frac{1}{r\sin\theta} \frac{\partial F}{\partial \phi}\hat{\phi}\]
**Definition 1.1.9 ** The **divergence** denoted $\nabla \cdot \vec{F}$ of a differentiable vector field $\vec{F}$ is a scalar field defined by the sum of partial derivatives of the components of the vector field.
\[\nabla \cdot \vec{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}\]\[\nabla \cdot \vec{F} = \frac{1}{r^2}\frac{\partial (r^2F_r)}{\partial r} + \frac{1}{r\sin\theta}\frac{\partial}{\partial \theta} \left(F_\theta \sin\theta\right) + \frac{1}{\sin\theta}\frac{\partial F_\phi}{\partial \phi}\]\[\nabla \cdot \vec{F} = \frac{1}{s}\frac{\partial (sF_s)}{\partial s} + \frac{1}{s} \frac{\partial F_\phi}{\partial \phi} + \frac{\partial F_z}{\partial z}\]
**Definition 1.1.10 ** The **curl** denoted $\nabla \cross \vec{F}$ of a differentiable vector field $\vec{F}$ is a vector field defined in terms of the following partial derivatives.
\[\nabla \times \vec{F}=\det\begin{pmatrix}
\hat{x} & \hat{y} & \hat{z}\\
\frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\
F_x & F_y & F_z
\end{pmatrix}=\left(\frac{\partial F_z}{\partial y}-\frac{\partial F_y}{\partial z}\right)\hat{x}+\left(\frac{\partial F_x}{\partial z}-\frac{\partial F_z}{\partial x}\right)\hat{y}+\left(\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}\right)\hat{z}\]\[\nabla \times \vec{F} = \frac{1}{r\sin\theta}\left( \frac{\partial }{\partial\theta}(F_\phi \sin\theta) - \frac{\partial F_\theta}{\partial \phi} \right)\hat{r} + \frac{1}{r}\left( \frac{1}{\sin\theta}\frac{\partial F_r}{\partial \phi} - \frac{\partial}{\partial r}(rF_\phi)\right)\hat{\theta} + \frac{1}{r}\left(\frac{\partial }{\partial r}(rF_\theta)-\frac{\partial F_r}{\partial \theta}\right)\]\[\nabla \times \vec{F} = \left( \frac{1}{s}\frac{\partial F_z}{\partial \phi} - \frac{\partial F_\phi}{\partial z} \right)\hat{s} + \left( \frac{\partial F_s}{\partial z} - \frac{\partial F_z}{\partial s} \right)\hat{\phi} + \frac{1}{s}\left(\frac{\partial (sF_\phi)}{\partial s} - \frac{\partial F_s}{\partial \phi} \right)\hat{z}\]
**Definition 1.1.11 ** The **Laplace** denoted $\nabla^2 F$ of a differentiable scalar field $F$ is the divergence of the gradient of $F$.
\[\nabla^2F = \nabla\cdot\nabla F = \frac{\partial^2 F}{\partial x^2} + \frac{\partial^2 F}{\partial y^2} + \frac{\partial^2 F}{\partial z^2}\]
**Proposition 1.1.12 ** The **curl of a gradient is zero**, that is $\nabla\times(\nabla F)=0$ for any scalar field $F$.
**Proposition 1.1.13 ** The **divergence of a curl is zero**, that is $\nabla\cdot(\nabla \times \vec{F})=0$ for any vector field $\vec{F}$.
**Proposition 1.1.14 ** The **curl of curl** can be written in terms of gradients and divergences for any vector field $\vec{F}$.
\[\nabla\times\left(\nabla\times\vec{F}\right) = \nabla\left( \nabla\cdot\vec{F} \right) - \nabla\cdot\nabla\vec{F} = \nabla\left( \nabla\cdot\vec{F} \right) - \nabla^2\vec{F}\]
**Theorem 1.1.15 ** The **gradient theorem** states that gradients are path independent, that is for any differentiable scalar field $F$,
\[\int_\vec{a}^\vec{b}(\nabla F)\cdot d\vec{\ell} = F(\vec{b})-F(\vec{a})\]
**Theorem 1.1.16 ** The **divergence theorem** or **Gauss's theorem** states that the surface integral of continuously differentiable vector field $\vec{F}$ dotted with the normal vector $d\vec{S}$ over the piecewise smooth boundary $S$ of a volume $V$ is the volume integral of the divergence of $\vec{F}$ over the volume $V$.
\[\iint_S \vec{F}\cdot d\vec{S} = \iiint_V(\nabla\cdot\vec{F})dV\]
**Theorem 1.1.17 ** The **curl theorem** or **Stokes' theorem** states that the loop integral of a continuously differentiable vector field $\vec{F}$ along the boundary path $P$ of a smooth oriented surface $S$ is the surface integral of the curl of $\vec{F}$ over the surface $S$.
\[\int_P\vec{F}\cdot d\vec{P} = \iint_S(\nabla\times\vec{F})\cdot d\vec{S}\]
**Definition 1.1.18 ** The **Dirac delta** denoted $\delta(x)$ is the notation for a distribution peaked infinitesimally around zero.
\[\delta(x) = \lim_{a\to 0} \frac{1}{|a|\sqrt{\pi}}e^{-(x/a)^2}\]
### 1.2 SI Units
**Definition 1.2.1 ** The **SI unit system** is the most popular system of units that uses the fundamental units of [seconds](https://kaedon.net/l/^ahc1#h5t8), [meters](https://kaedon.net/l/^ahc1#8dza), [kilograms](https://kaedon.net/l/^ahc1#wahe), [ampere](https://kaedon.net/l/^ahc1#613r) and [Kelvin](https://kaedon.net/l/^ahc1#ncp0) to derive a system of units to describe the universe.
**Definition 1.2.2 ** A **second** (**s**) is the SI unit of time that is exactly 9192631770 hyperfine transitions of a Caesium-133 atom.
**Definition 1.2.3 ** A **meter** (**m**) is the SI unit of distance that is exactly the distance light travels in $1/299792458$ seconds.
**Definition 1.2.4 ** A **kilogram** (**kg**) is the SI unit of mass defined exactly by fixing Plank's constant $h=6.62607015 \times 10^{−34}\text{kg } \text{m}^2\text{s}^{−1}$.
**Definition 1.2.5 ** An **ampere** (**A**) is the SI unit of current that is exactly the flow of $10^{19}/1.602176634$ protons per second.
**Definition 1.2.6 ** A **Kelvin** (**K**) is the SI unit of absolute temperature defined exactly by fixing Boltzmann's constant $k=1.380649\times 10^{-23}\text{kg }\text{m}^2 \text{s}^{-2}\text{K}^{-1}$.
**Definition 1.2.7 ** A **Coulomb** (**C**) is the SI unit of charge defined by $\text{C} = \text{A s}$ or exactly $10^{19}/1.602176634$ protons.
**Definition 1.2.8 ** A **Newton** (**N**) is the SI unit of force defined by $\text{N} = \text{kg m}/\text{s}^{2}$.
**Definition 1.2.9 ** A **Joule** (**J**) is the SI unit of energy defined by $\text{J} = \text{N m} = \text{kg }\text{m}^{2}/\text{s}^{2}$.
**Definition 1.2.10 ** A **Watt** (**w**) is the SI unit of power defined by $\text{w} = \text{J}/\text{s}$.
**Definition 1.2.11 ** A **Pascal** (**Pa**) is the SI unit of pressure defined by $\text{Pa}=\text{N}/\text{m}^2 = \text{J}/\text{m}^3 = \text{kg }\text{m}^{-1}\text{s}^{-2}$.
**Definition 1.2.12 ** A **Volt** (**V**) is the SI unit of electric potential defined by $\text{V} = \text{J}/\text{C} = \text{w}/\text{A} = \text{kg }\text{m}^2\text{s}^{-3}\text{A}^{-1}$.
**Definition 1.2.13 ** A **Volt per Meter** (**V/m**) is the SI unit of electric field defined by $\text{V}/\text{m} = \text{N}/\text{C} = \text{kg m}\text{s}^{-2}\text{A}^{-1}$.
**Definition 1.2.14 ** A **Telsa** (**T**) is the SI unit of magnetic field defined by $\text{T} = \text{V s}/\text{m}^2 = \text{kg }\text{s}^{-2}\text{A}^{-1}$.
**Definition 1.2.15 ** The **fine structure constant** denoted $\alpha$ is a dimensionless experimentally determined constant defined below. In any system of units, the fine structure constant is dimensionless and therefore has the same value:
\[\alpha = \frac{\mu_0 e^2 c}{2 h} = \frac{e^2}{2\varepsilon_0 h c} \approx 0.0072973525643 \approx 1/137.035999177\]
**Law 1.2.16 ** **Maxwell's Equations** are a set of coupled differential equations that form the foundations of classical electromagnetism.
\[\nabla\cdot \vec{E} = \frac{\rho}{\varepsilon_0}\]
\[\nabla\cdot \vec{B} = 0\]
\[\nabla\times\vec{E} = -\frac{\partial \vec{B}}{\partial t}\]
\[\nabla\times \vec{B} = \mu_0\left( \vec{J} + \varepsilon_0\frac{\partial \vec{E}}{\partial t} \right)\]
**Definition 1.2.17 ** The **vacuum permittivity** $\varepsilon_0$ is the physical constant defined in terms of the fine structure constant $\alpha$, charge of an electron $e$, Plank constant $h$ and speed of light $c$.
\[\varepsilon_0 = \frac{e^2}{2\alpha hc}\]
**Definition 1.2.18 ** The **vacuum permeability** $\mu_0$ is the physical constant defined in terms of the fine structure constant $\alpha$, charge of an electron $e$, Plank constant $h$ and speed of light $c$.
\[\mu_0 = \frac{2\alpha h}{e^2c}\]
**Result 1.2.19 ** The **product of vacuum permittivity and vacuum permeability** is the reciprocal of the speed of light squared.
\[\varepsilon_0\mu_0 = \frac{1}{c^2}\]
### 1.3 Maxwell's Equations
**Law 1.3.1 ** **Maxwell's Equations** are a set of coupled differential equations that form the foundations of classical electromagnetism.
\[\nabla\cdot \vec{E} = \frac{\rho}{\varepsilon_0}\]
\[\nabla\cdot \vec{B} = 0\]
\[\nabla\times\vec{E} = -\frac{\partial \vec{B}}{\partial t}\]
\[\nabla\times \vec{B} = \mu_0\left( \vec{J} + \varepsilon_0\frac{\partial \vec{E}}{\partial t} \right)\]
**Definition 1.3.2 ** The **vacuum permittivity** $\varepsilon_0$ is the physical constant defined in terms of the fine structure constant $\alpha$, charge of an electron $e$, Plank constant $h$ and speed of light $c$.
\[\varepsilon_0 = \frac{e^2}{2\alpha hc}\]
**Definition 1.3.3 ** The **vacuum permeability** $\mu_0$ is the physical constant defined in terms of the fine structure constant $\alpha$, charge of an electron $e$, Plank constant $h$ and speed of light $c$.
\[\mu_0 = \frac{2\alpha h}{e^2c}\]
**Result 1.3.4 ** The **product of vacuum permittivity and vacuum permeability** is the reciprocal of the speed of light squared.
\[\varepsilon_0\mu_0 = \frac{1}{c^2}\]
## 2 Electrostatics
### 2.1 Electric Field
**Definition 2.1.1 ** The **electric field** denoted $\vec{E}(\vec{r})$ is a vector field of the force that would be felt by a test charge at a point in space. The units of electric field are Newtons per Coulomb denoted $N/C$. For a charge $q$ at position $\vec{r}$ the force $\vec{F}$ from electric field $\vec{E}$ can be calculated with the following equation:
\[\vec{F} = q\vec{E}(\vec{r})\]
**Definition 2.1.2 ** The **electric displacement field** denoted $\vec{D}$ is defined in terms of the electric field $\vec{E}$ the polarization $\vec{P}$.
\[\vec{D} = \varepsilon_0\vec{E} + \vec{P}\]
**Definition 2.1.3 ** The **polarization** denoted $\vec{P}$ is the [electric dipole moment](https://kaedon.net/l/^ahc1#wr8f) per unit volume of the bound charge density $\rho_b$ in a material.
\[\vec{P} = \frac{d\vec{p}}{dV}\]
\[- \nabla\cdot\vec{P} = \rho_b\]
**Law 2.1.4 ** **Coulomb's law** states that the force $\vec{F}$ on a point charge $q_1$ located at $\vec{r}_1$ due to another point charge $q_2$ located at $\vec{r}_2$ can be obtained with the following equation: $\newcommand\abs[1]{\left|#1\right|}$
\[\vec{F} = \frac{1}{4\pi\varepsilon_0}q_1q_2\frac{\vec{r}_1-\vec{r}_2}{\abs{\vec{r}_1-\vec{r}_2}^3}\]
**Result 2.1.5 ** The **electric field of a point charge** $q_1$ located at $\vec{r}_1$ can be directly obtained from coulomb's law.$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{E}(\vec{r}) = \frac{1}{4\pi\varepsilon_0}q_1\frac{\vec{r}-\vec{r}_1}{\abs{\vec{r}-\vec{r}_1}^3}\]
**Result 2.1.6 ** The **electric field of many point charges** $q_1,\dots,q_n$ located at $\vec{r}_1,\dots,\vec{v}_n$ can be directly obtained from coulomb's law.$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{E}(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\sum_{i=1}^n{q_i}\frac{\vec{r}-\vec{r}_i}{\abs{\vec{r}-\vec{r}_i}^3}\]
**Definition 2.1.7 ** A **charge density** denoted $\rho(\vec{r})$ is the function whose integral represents the charge in a region of space.
**Result 2.1.8 ** The **electric field of a charge density** $\rho$ can be obtained by direct integration.$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{E}(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int{ \rho(\vec{r}') \frac{\vec{r}-\vec{r}'}{\abs{\vec{r}-\vec{r}'}^3} d^3r'}\]
**Law 2.1.9 ** **Gauss's law** states that states that the surface integral of the electric field $\vec{E}$ dotted with the normal vector $\vec{n}$ over a piecewise smooth boundary $S$ of a volume $V$ is the volume integral of the charge density $\rho$ over a volume $V$.
\[\iint_S (\vec{E}\cdot \vec{n}) d^2r = \frac{1}{\varepsilon_0}\iiint_V\rho(\vec{r})d^3r\]
**Result 2.1.10 ** **Gauss's law for discrete charges** states that for discrete charges the volume integral can be simplified into a sum of the chargest inside the volume.
\[\iint_S (\vec{E}\cdot \vec{n}) d^2r = \frac{1}{\varepsilon_0}\sum_i{q_i}\]
### 2.2 Electric Potential
**Definition 2.2.1 ** The **electric potential** or **voltage** denoted $V(\vec{r},t)$ is a scalar potential such that the negative gradient is the electric field in electrostatic systems.
\[\vec{E} = -\nabla V - \frac{\partial \vec{A}}{\partial t}\]
**Result 2.2.2 ** The **electric potential of a charge density** can be obtained by direct integration.$\newcommand\abs[1]{\left|#1\right|}$
\[V(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int{ \frac{\rho(\vec{r}')}{\abs{\vec{r}-\vec{r}'}} d^3r'}\]
**Result 2.2.3 ** The **electric fields near a surface charge distribution** are discontinuous in the direction normal $\vec{n}$ to the surface charge density $\sigma$.
\[(\vec{E}_{out}-\vec{E}_{in})\cdot\vec{n} = \sigma(\vec{r})/\varepsilon_0\]
**Result 2.2.4 ** The **electric potentials near a surface dipole layer**, with dipole moment $\vec{D}(\vec{r})$ in the direction normal to the surface, are discontinuous proportional to the dipole moment $D(\vec{r})$.
\[V_2-V_1 = D(\vec{r})/\varepsilon_0\]
**Result 2.2.5 ** The **potential energy of many point charges** $W$ is the total energy of a set of many point charges $q_1,\dots,q_n$ at positions $\vec{r}_1,\dots,\vec{r}_n$ due to the forces acting between them.$\newcommand\abs[1]{\left|#1\right|}$
\[W = \frac{1}{8\pi\varepsilon_0}\sum_i\sum_j\frac{q_iq_j}{\abs{\vec{r}_i-\vec{r}_j}}\]
**Result 2.2.6 ** The **potential energy of a charge distribution** $W$ is the total energy of a charge distribution $\rho(\vec{r})$.$\newcommand\abs[1]{\left|#1\right|}$
\[W = \frac{1}{8\pi\varepsilon_0}\int\int\frac{\rho(\vec{r})\rho(\vec{r}')}{\abs{\vec{r}-\vec{r}'}}d^3r\ d^3r' = \frac{\varepsilon_0}{2}\int\abs{\vec{E}}^2d^3r\]
### 2.3 Spherical Harmonics
**Definition 2.3.1 ** The **Legendre polynomials** $P_\ell(x)$ are a set of polynomials defined on the interval $-1\leq x \leq 1$ for $\ell \in \{0,1,2,\dots\}$ by the following expression.
\[P_\ell(x) = \frac{1}{2^\ell}\]
**Definition 2.3.2 ** The **associated Legendre polynomials** $P_\ell^m(x)$ are a set of polynomials defined on the interval $-1\leq x \leq 1$ for $\ell \in \{0,1,2,3,\dots\}$ and $m \in \{-\ell,-\ell+1,\dots,0,\dots,\ell-1,\ell\}$ by the following expression.
\[P_\ell^m(x) = \frac{(-1)^{m}}{2^\ell\ell!}(1-x^2)^{m/2}\frac{d^{\ell+m}}{dx^{\ell+m}}(x^2-1)^\ell\]
**Definition 2.3.3 ** The **spherical harmonics** $Y_{\ell,m}(\theta,\phi)$ are a set of spherical functions defined for $\ell \in \{0,1,2,3,\dots\}$ and $m \in \{-\ell,-\ell+1,\dots,0,\dots,\ell-1,\ell\}$ that forms an orthonormal bases for the set of complex spherical functions.
\[Y_{\ell,m}(\theta,\phi) = \sqrt{\frac{2\ell+1}{4\pi}\frac{(\ell-m)!}{(\ell+m)!}} P_\ell^m(\cos\theta)e^{im\phi}\]
**Result 2.3.4 ** **Properties of Spherical Harmonics:** The spherical harmonics $Y_{\ell,m}$ and $Y_{\ell, -m}$ are related by the following relation,
\[Y_{\ell,-m}(\theta,\phi) = (-1)^{m}Y_{\ell,m}^*(\theta, \phi)\]
Spherical harmonics from an orthonormal basis with the following orthogonality and normalization conditions,
\[\int_0^{2\pi}\int_0^\pi Y^*_{\ell,m'}(\theta,\phi)Y_{\ell,m}(\theta,\phi) \sin\theta\ d\theta\ d\phi = \delta_{\ell',\ell}\delta_{m',m}\]
Spherical harmonics span the set of all complex spherical functions as show by the following completeness relation,
\[\sum_{\ell = 0}^\infty \sum_{m=-\ell}^\ell Y_{\ell,m}^*(\theta',\phi')Y_{\ell,m}(\theta,\phi) = \delta(\phi-\phi')\delta(\cos\theta-\cos\theta')\]
**Table 2.3.5 ** **Table of Spherical Harmoincs**
\[Y_{0,0} = \frac{1}{\sqrt{4\pi}}\]
\[Y_{1,1} = -\sqrt{\frac{3}{8\pi}}\sin\theta\ e^{i\phi}\]
\[Y_{1,0} = \sqrt{\frac{3}{4\pi}}\cos\theta\]
\[Y_{2,2} = \frac{1}{4}\sqrt{\frac{15}{2\pi}} \sin^2\theta\ e^{2i\phi}\]
\[Y_{2,1} = -\sqrt{\frac{15}{8\pi}}\sin\theta\cos\theta\ e^{i\phi}\]
\[Y_{2,0} = \sqrt{\frac{5}{4\pi}}\left(\frac{3}{2}\cos^2\theta - \frac{1}{2}\right)\]
### 2.4 Electric Multipole Expansion
**Theorem 2.4.1 ** The **multipole expansion theorem** states that for a charge distribution localized within a sphere, the electric potential outside the sphere can be written in terms of spherical harmonics.
\[V(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\sum_{\ell=0}^\infty\sum_{m=-\ell}^\ell\frac{4\pi}{2\ell+1}q_{\ell,m}\frac{Y_{\ell,m}(\theta,\phi)}{r^{\ell+1}}\]
\[q_{\ell,m} = \int Y^*_{\ell,m}(\theta,\phi)r^{\ell}\rho(\vec{r})d^3r\]
**Result 2.4.2 ** The multipole moment $q_{\ell,m}$ and $q_{\ell, -m}$ are related by the relation $q_{\ell,-m} = (-1)^{m}q^*_{\ell,m}$.
**Definition 2.4.3 ** The **monopole moment** $q$ of a charge distribution $\rho(\vec{r})$ is simply the total charge.
\[q = \int \rho(\vec{r}) d^3r\]
**Definition 2.4.4 ** The **dipole moment** $\vec{p}$ of a charge distribution $\rho(\vec{r})$ is defined with the following integral.
\[\vec{p} = \int\vec{r}\rho(\vec{r})d^3r\]
**Definition 2.4.5 ** The **quadrupole moment** $Q$ of a charge distribution $\rho(\vec{r})$ is a $3$ by $3$ matrix with components $Q_{j,k}$ defined with the following integral.
\[Q_{j,k} = \int \left[3r_jr_k-r^2\delta_{j,k}\right]\rho(\vec{r})d^3r\]
**Result 2.4.6 ** The multipole expansion of a charge distribution can be written in terms of the multiple moments of the charge distribution. The first 6 terms of the multiple expansion are written below in terms of the monopole moment $q$, the dipole moment $\vec{p}$ and the quadrupole moment $Q$ of a charge distribution $\rho(\vec{r})$.
\[q_{0,0} = \frac{1}{\sqrt{4\pi}}\int\rho(\vec{r})d^3r = \frac{1}{\sqrt{4\pi}}q\]
\[q_{1,1} = -\sqrt{\frac{3}{8\pi}}\int(x-iy)\rho(\vec{r})d^3r = -\sqrt{\frac{3}{8\pi}}(p_x-ip_y)\]
\[q_{1,0} = \sqrt{\frac{3}{4\pi}}\int z\rho(\vec{r})d^3r = \sqrt{\frac{3}{4\pi}}p_z\]
\[q_{2,2} = \frac{1}{4}\sqrt{\frac{15}{2\pi}}\int(x-iy)\rho(\vec{r})d^3r = \frac{1}{12}\sqrt{\frac{15}{2\pi}}(Q_{1,1}-2iQ_{1,2}-Q_{2,2})\]
\[q_{2,1} = -\sqrt{\frac{15}{8\pi}}\int z(x-iy)\rho(\vec{r})d^3r = -\frac{1}{3}\sqrt{\frac{15}{8\pi}}(Q_{1,3}-iQ_{2,3})\]
\[q_{2,0} = \frac{1}{2}\sqrt{\frac{5}{4\pi}}\int(3z^2-r^2)\rho(\vec{r})d^3r = \frac{1}{2}\sqrt{\frac{5}{4\pi}}Q_{3,3}\]
### 2.5 Cartesian Separation of Variables
**Theorem 2.5.1 ** The solution $y(x)$ to a **second order linear differential equation** of the form
\[a\frac{d^2 y(x)}{dx^2} + b\frac{d y(x)}{dx} + c y(x) = 0\]
is $y=Ae^{r_1x} + Be^{r_2x}$ for some constants $A,B\in\mathbb{C}$ and where $r_1,r_2\in\mathbb{C}$ are the two solutions to the quadratic equation $ar^2 + br + c = 0$.
**Corollary 2.5.2 ** An equation of the form $\frac{1}{y(x)}\frac{d^2 y(x)}{dx^2} = k$ has solution $y(x) = Ae^{\sqrt{k}x} + Be^{-\sqrt{k}x}$ for some constants $A,B\in\mathbb{C}$.
**Definition 2.5.3 ** **Separation of variables** is a technique solve differential equations by algebraically separating the equation into independent one dimensional differential equations.
**Definition 2.5.4 ** The **Laplace equation** is for a scalar function $V(\vec{r})$ is the second-order partial differential equation defined by
\[\nabla^2V(\vec{r}) = 0\]
where $\nabla^2$ is the [Laplace operator](https://kaedon.net/l/^pd4j#59d9). This equation describes how an electrostatic potential function behaves in a region with zero charge density.
**Theorem 2.5.5 ** The **uniqueness theorem for the Laplace equation** states that for a
**Result 2.5.6 ** The **Laplace equation written in Cartesian coordinates** for a potential $V(x,y,z)$ is
\[\nabla^2 V(\vec{r}) = \frac{\partial^2 V(\vec{r})}{\partial x^2} + \frac{\partial^2 V(\vec{r})}{\partial y^2} + \frac{\partial^2 V(\vec{r})}{\partial z^2} = 0\]
**Result 2.5.7 ** Applying **separation of variables for the Laplace equation in Cartesian coordinates** and assuming that the solution is in product form $V(x,y,z) = X(x)Y(y)Z(z)$, produces the following differential equations.
\[\frac{1}{X}\frac{d^2 X}{d x^2} + \frac{1}{Y}\frac{d^2 Y}{d y^2} + \frac{1}{Z}\frac{d^2 Z}{d z^2} = 0\]
\[\frac{1}{X}\frac{d^2 X}{d x^2} = k_x,\quad \frac{1}{Y}\frac{d^2 Y}{d y^2} = k_y,\quad \frac{1}{Z}\frac{d^2 Z}{d z^2} = k_z\]
### 2.6 Spherical Separation of Variables
**Result 2.6.1 ** The **Laplace equation in spherical coordinates** for a potential $V(r,\theta,\phi)$ is
\[\frac{1}{r}\frac{\partial^2}{\partial r^2}(rV(\vec{r})) + \frac{1}{r^2\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\ \frac{\partial V(\vec{r})}{\partial \theta}\right) + \frac{1}{r^2\sin^2\theta} \frac{\partial^2V(\vec{r})}{\partial \phi} = 0\]
**Result 2.6.2 ** Applying **separation of variables for the Laplace equation in Spherical coordinates** and assuming that the solution is in product form $V(r,\theta,\phi) = \frac{U(r)}{r}P(\theta)Q(\phi)$, produces the following differential equation.
\[r^2\sin^2\theta\left[ \frac{1}{U}\frac{d^2 U}{dr^2} + \frac{1}{Pr^2\sin\theta}\frac{d}{d\theta}\left(\sin\theta\ \frac{dP}{d\theta}\right) \right] + \frac{1}{Q}\frac{d^2Q}{d\phi^2} = 0\]
From this it can be shown that any solution can be written in terms of spherical harmonics with coefficients $A_{\ell,m},B_{\ell,m}\in\mathbb{R}$.
\[V(r,\theta,\phi) = \sum_{\ell=0}^\infty{\sum_{m=-\ell}^\ell{\left[ A_{\ell,m} r^\ell + \frac{B_{\ell,m}}{r^{\ell+1}} \right]Y_{\ell,m}(\theta,\phi)}}\]
\[A_{\ell,m}a^{\ell} + \frac{B_{\ell,m}}{a^{\ell+1}} = \int Y^*_{\ell,m}(\theta,\phi)V(r=a,\theta,\phi)d\Omega\]
**Corollary 2.6.3 ** A **Legendre polynomial solution to the Laplace equation in spherical coordinates** for systems with azimuthal symmetry can be written in terms of [Legendre polynomials](https://kaedon.net/l/^ahc1#85ep) $P_\ell$ with coefficients $A_{\ell,m},B_{\ell,m}\in\mathbb{R}$.
\[V(r,\theta) = \sum_{\ell = 0}^\infty\left[A_{\ell,m} r^\ell + \frac{B_{\ell,m}}{r^{\ell+1}}\right]P_\ell(\cos\theta)\]
### 2.7 Cylindrical Separation of Variables
**Result 2.7.1 ** The **Laplace equation in cylindrical coordinates** for a potential $V(s,\phi,z)$ is
\[\frac{\partial^2 V(\vec{r})}{\partial s^2} + \frac{1}{s}\frac{\partial V(\vec{r})}{\partial s} + \frac{1}{s^2}\frac{\partial^2 V(\vec{r})}{d\phi^2} + \frac{\partial^2 V(\vec{r})}{\partial z^2} = 0\]
**Result 2.7.2 ** Applying **separation of variables for the Laplace equation in cylindrical coordinates** and assuming that the solution is in product form $V(s,\phi,z) = S(s)Q(\phi)Z(z)$, produces the following system of differential equations for some constants $k,v\in\mathbb{R}$.
\[\frac{1}{Z(z)}\frac{\partial^2 Z(z)}{\partial z^2} = k^2\]
\[\frac{1}{Q(\phi)}\frac{\partial^2 Q(\phi)}{\partial \phi^2} = -v^2\]
\[\frac{\partial^2 S(s)}{\partial s^2} + \frac{1}{s}\frac{\partial S(s)}{\partial s} + \left(k^2 - \frac{v^2}{s^2}\right)S(s) = 0\]
**Definition 2.7.3 ** The **Bessel functions** are the canonical solutions $y(x)$ of **Bessel's differential equation**, defined below for some complex number $\alpha$.
\[x^2\frac{d^2y}{dx^2} + x\frac{dy}{dx} + (x^2 - \alpha^2)y = 0\]
**Corollary 2.7.4 ** The third differential equation in separation of variables for the Laplace equation in cylindrical coordinates can be written as Bessel's differential equation where $x=ks$ and $\alpha = v$,
\[x^2\frac{d^2y}{dx^2} + x\frac{dy}{dx} + (x^2 - v^2)y = 0\]
\[\frac{d^2y}{dx^2} + \frac{1}{x}\frac{dy}{dx} + \left(1 - \frac{v^2}{x^2}\right)y = 0\]
**Definition 2.7.5 ** The **Bessel functions of the first kind** denoted $J_\alpha(x)$ are solutions of Bessel's differential equation for $\alpha\in\mathbb{C}$ defined by the following equation where $\Gamma$ is the gamma function.
\[J_{\alpha}(x) = \sum_{n=0}^\infty\frac{(-1)^n}{n!\Gamma(n+\alpha+1)}\left(\frac{x}{2}\right)^{2n+\alpha}\]
**Definition 2.7.6 ** The **Bessel functions of the second kind** or **Neumann functions** denoted $N_\alpha(x)$ are solutions of Bessel's differential equation for $\alpha\in\mathbb{C}$ defined by the following equation where $J_\alpha$ are the Bessel functions of the first kind.
\[N_\alpha(x) = \frac{J_\alpha(x)\cos(\alpha\pi) - J_{-\alpha}(x)}{\sin(\alpha\pi)}\]
**Definition 2.7.7 ** The **Bessel functions of the third kind** or **Hankel functions** denoted $H_\alpha^{(1)}(x),H_\alpha^{(2)}(x)$ are solutions of Bessel's differential equation for $\alpha\in\mathbb{C}$ defined by the following equation where $J_\alpha$ and $N_{\alpha}$ are Bessel functions of the first and second kind respectively.
\[H_\alpha^{(1)}(x) = J_\alpha(x) + i N_\alpha(x)\]
\[H_\alpha^{(2)}(x) = J_\alpha(x) - i N_\alpha(x)\]
### 2.8 Method of Relaxation
**Definition 2.8.1 ** The **method of relaxation** is a numerical method for solving the Laplace equation for a finite region of space with known boundary conditions iteratively. This method computes the potential $V(\vec{r})$ at a finite number of point by iteratively setting each point to the average of the points around it.
| | |
|:--|:--|
| $s = \sqrt{x^2+y^2}\quad$ | $\hat{s} = \cos(\phi)\hat{x} + \sin(\phi)\hat{y}$ |
| $\phi = \tan^{-1}(y/x)\quad$ | $\hat{\phi} = -\sin(\phi)\hat{x} + \cos(\phi)\hat{y}$ |
| $z=z\quad$ | $\hat{z}=\hat{z}$ |
| $\ $ | $\ $ |
| $x = s\cos\phi\quad$ | $\hat{x} = \cos(\phi)\hat{s} - \sin(\phi)\hat{\phi}$ |
| $y = s\sin\phi\quad$ | $\hat{y} = \sin(\phi)\hat{s} + \cos(\phi)\hat{\phi}$ |
| $z=z\quad$ | $\hat{z}=\hat{z}$ |
**File 1.1.3 ** Cylindrical.PNG
**Definition 1.1.4 ** The **Kronecker delta** $\delta_{ij} = \left\{\begin{array}{lr}
1, & \text{if } i = j\\
0, & \text{if } i\neq j
\end{array}\right\}$.
**Definition 1.1.5 ** The **Levi-Civita symbol** $\varepsilon_{a_1,a_2,\dots,a_n} = \left\{\begin{array}{rl}
+1, & \text{if } (a_1,a_2,\dots,a_n)\text{ is an even permutation of }(1,2,\dots,n)\\
-1, & \text{if } (a_1,a_2,\dots,a_n)\text{ is an odd permutation of }(1,2,\dots,n)\\
0, & \text{otherwise}
\end{array}\right\}$
**Definition 1.1.6 ** The **dot product** denoted $\vec{a}\cdot\vec{b}$ of two vectors $\vec{a}$ and $\vec{b}$ is the sum of the products of there components in any orthonormal basis.
\[\vec{a}\cdot\vec{b} = \sum_{i}a_ib_i\]
**Definition 1.1.7 ** The **cross product** of two vectors $\vec{a}$ and $\vec{b}$ is defined by the following sums of the products of there components in any orthonormal basis $\vec{e_1},\vec{e_2},\dots,\vec{e_n}$.
\[\vec{a}\times\vec{b} = \sum_i\sum_j\sum_k\varepsilon_{ijk}a_jb_k \vec{e_i}\]
**Definition 1.1.8 ** The **gradient** denoted $\nabla F$ of a differentiable scalar field $F$ is the vector field defined by the partial derivatives of the scalar field.
\[\nabla F = \frac{\partial F}{\partial x}\hat{x} + \frac{\partial F}{\partial y}\hat{y} + \frac{\partial F}{\partial z}\hat{z}=\left(\frac{\partial F}{\partial x},\frac{\partial F}{\partial y},\frac{\partial F}{\partial z}\right)\]\[\nabla F = \frac{\partial F}{\partial r}\hat{r} + \frac{1}{r}\frac{\partial F}{\partial \theta}\hat{\theta} + \frac{1}{r\sin\theta} \frac{\partial F}{\partial \phi}\hat{\phi}\]
**Definition 1.1.9 ** The **divergence** denoted $\nabla \cdot \vec{F}$ of a differentiable vector field $\vec{F}$ is a scalar field defined by the sum of partial derivatives of the components of the vector field.
\[\nabla \cdot \vec{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}\]\[\nabla \cdot \vec{F} = \frac{1}{r^2}\frac{\partial (r^2F_r)}{\partial r} + \frac{1}{r\sin\theta}\frac{\partial}{\partial \theta} \left(F_\theta \sin\theta\right) + \frac{1}{\sin\theta}\frac{\partial F_\phi}{\partial \phi}\]\[\nabla \cdot \vec{F} = \frac{1}{s}\frac{\partial (sF_s)}{\partial s} + \frac{1}{s} \frac{\partial F_\phi}{\partial \phi} + \frac{\partial F_z}{\partial z}\]
**Definition 1.1.10 ** The **curl** denoted $\nabla \cross \vec{F}$ of a differentiable vector field $\vec{F}$ is a vector field defined in terms of the following partial derivatives.
\[\nabla \times \vec{F}=\det\begin{pmatrix}
\hat{x} & \hat{y} & \hat{z}\\
\frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\
F_x & F_y & F_z
\end{pmatrix}=\left(\frac{\partial F_z}{\partial y}-\frac{\partial F_y}{\partial z}\right)\hat{x}+\left(\frac{\partial F_x}{\partial z}-\frac{\partial F_z}{\partial x}\right)\hat{y}+\left(\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}\right)\hat{z}\]\[\nabla \times \vec{F} = \frac{1}{r\sin\theta}\left( \frac{\partial }{\partial\theta}(F_\phi \sin\theta) - \frac{\partial F_\theta}{\partial \phi} \right)\hat{r} + \frac{1}{r}\left( \frac{1}{\sin\theta}\frac{\partial F_r}{\partial \phi} - \frac{\partial}{\partial r}(rF_\phi)\right)\hat{\theta} + \frac{1}{r}\left(\frac{\partial }{\partial r}(rF_\theta)-\frac{\partial F_r}{\partial \theta}\right)\]\[\nabla \times \vec{F} = \left( \frac{1}{s}\frac{\partial F_z}{\partial \phi} - \frac{\partial F_\phi}{\partial z} \right)\hat{s} + \left( \frac{\partial F_s}{\partial z} - \frac{\partial F_z}{\partial s} \right)\hat{\phi} + \frac{1}{s}\left(\frac{\partial (sF_\phi)}{\partial s} - \frac{\partial F_s}{\partial \phi} \right)\hat{z}\]
**Definition 1.1.11 ** The **Laplace** denoted $\nabla^2 F$ of a differentiable scalar field $F$ is the divergence of the gradient of $F$.
\[\nabla^2F = \nabla\cdot\nabla F = \frac{\partial^2 F}{\partial x^2} + \frac{\partial^2 F}{\partial y^2} + \frac{\partial^2 F}{\partial z^2}\]
**Proposition 1.1.12 ** The **curl of a gradient is zero**, that is $\nabla\times(\nabla F)=0$ for any scalar field $F$.
**Proposition 1.1.13 ** The **divergence of a curl is zero**, that is $\nabla\cdot(\nabla \times \vec{F})=0$ for any vector field $\vec{F}$.
**Proposition 1.1.14 ** The **curl of curl** can be written in terms of gradients and divergences for any vector field $\vec{F}$.
\[\nabla\times\left(\nabla\times\vec{F}\right) = \nabla\left( \nabla\cdot\vec{F} \right) - \nabla\cdot\nabla\vec{F} = \nabla\left( \nabla\cdot\vec{F} \right) - \nabla^2\vec{F}\]
**Theorem 1.1.15 ** The **gradient theorem** states that gradients are path independent, that is for any differentiable scalar field $F$,
\[\int_\vec{a}^\vec{b}(\nabla F)\cdot d\vec{\ell} = F(\vec{b})-F(\vec{a})\]
**Theorem 1.1.16 ** The **divergence theorem** or **Gauss's theorem** states that the surface integral of continuously differentiable vector field $\vec{F}$ dotted with the normal vector $d\vec{S}$ over the piecewise smooth boundary $S$ of a volume $V$ is the volume integral of the divergence of $\vec{F}$ over the volume $V$.
\[\iint_S \vec{F}\cdot d\vec{S} = \iiint_V(\nabla\cdot\vec{F})dV\]
**Theorem 1.1.17 ** The **curl theorem** or **Stokes' theorem** states that the loop integral of a continuously differentiable vector field $\vec{F}$ along the boundary path $P$ of a smooth oriented surface $S$ is the surface integral of the curl of $\vec{F}$ over the surface $S$.
\[\int_P\vec{F}\cdot d\vec{P} = \iint_S(\nabla\times\vec{F})\cdot d\vec{S}\]
**Definition 1.1.18 ** The **Dirac delta** denoted $\delta(x)$ is the notation for a distribution peaked infinitesimally around zero.
\[\delta(x) = \lim_{a\to 0} \frac{1}{|a|\sqrt{\pi}}e^{-(x/a)^2}\]
### 1.2 SI Units
**Definition 1.2.1 ** The **SI unit system** is the most popular system of units that uses the fundamental units of [seconds](https://kaedon.net/l/^ahc1#h5t8), [meters](https://kaedon.net/l/^ahc1#8dza), [kilograms](https://kaedon.net/l/^ahc1#wahe), [ampere](https://kaedon.net/l/^ahc1#613r) and [Kelvin](https://kaedon.net/l/^ahc1#ncp0) to derive a system of units to describe the universe.
**Definition 1.2.2 ** A **second** (**s**) is the SI unit of time that is exactly 9192631770 hyperfine transitions of a Caesium-133 atom.
**Definition 1.2.3 ** A **meter** (**m**) is the SI unit of distance that is exactly the distance light travels in $1/299792458$ seconds.
**Definition 1.2.4 ** A **kilogram** (**kg**) is the SI unit of mass defined exactly by fixing Plank's constant $h=6.62607015 \times 10^{−34}\text{kg } \text{m}^2\text{s}^{−1}$.
**Definition 1.2.5 ** An **ampere** (**A**) is the SI unit of current that is exactly the flow of $10^{19}/1.602176634$ protons per second.
**Definition 1.2.6 ** A **Kelvin** (**K**) is the SI unit of absolute temperature defined exactly by fixing Boltzmann's constant $k=1.380649\times 10^{-23}\text{kg }\text{m}^2 \text{s}^{-2}\text{K}^{-1}$.
**Definition 1.2.7 ** A **Coulomb** (**C**) is the SI unit of charge defined by $\text{C} = \text{A s}$ or exactly $10^{19}/1.602176634$ protons.
**Definition 1.2.8 ** A **Newton** (**N**) is the SI unit of force defined by $\text{N} = \text{kg m}/\text{s}^{2}$.
**Definition 1.2.9 ** A **Joule** (**J**) is the SI unit of energy defined by $\text{J} = \text{N m} = \text{kg }\text{m}^{2}/\text{s}^{2}$.
**Definition 1.2.10 ** A **Watt** (**w**) is the SI unit of power defined by $\text{w} = \text{J}/\text{s}$.
**Definition 1.2.11 ** A **Pascal** (**Pa**) is the SI unit of pressure defined by $\text{Pa}=\text{N}/\text{m}^2 = \text{J}/\text{m}^3 = \text{kg }\text{m}^{-1}\text{s}^{-2}$.
**Definition 1.2.12 ** A **Volt** (**V**) is the SI unit of electric potential defined by $\text{V} = \text{J}/\text{C} = \text{w}/\text{A} = \text{kg }\text{m}^2\text{s}^{-3}\text{A}^{-1}$.
**Definition 1.2.13 ** A **Volt per Meter** (**V/m**) is the SI unit of electric field defined by $\text{V}/\text{m} = \text{N}/\text{C} = \text{kg m}\text{s}^{-2}\text{A}^{-1}$.
**Definition 1.2.14 ** A **Telsa** (**T**) is the SI unit of magnetic field defined by $\text{T} = \text{V s}/\text{m}^2 = \text{kg }\text{s}^{-2}\text{A}^{-1}$.
**Definition 1.2.15 ** The **fine structure constant** denoted $\alpha$ is a dimensionless experimentally determined constant defined below. In any system of units, the fine structure constant is dimensionless and therefore has the same value:
\[\alpha = \frac{\mu_0 e^2 c}{2 h} = \frac{e^2}{2\varepsilon_0 h c} \approx 0.0072973525643 \approx 1/137.035999177\]
**Law 1.2.16 ** **Maxwell's Equations** are a set of coupled differential equations that form the foundations of classical electromagnetism.
\[\nabla\cdot \vec{E} = \frac{\rho}{\varepsilon_0}\]
\[\nabla\cdot \vec{B} = 0\]
\[\nabla\times\vec{E} = -\frac{\partial \vec{B}}{\partial t}\]
\[\nabla\times \vec{B} = \mu_0\left( \vec{J} + \varepsilon_0\frac{\partial \vec{E}}{\partial t} \right)\]
**Definition 1.2.17 ** The **vacuum permittivity** $\varepsilon_0$ is the physical constant defined in terms of the fine structure constant $\alpha$, charge of an electron $e$, Plank constant $h$ and speed of light $c$.
\[\varepsilon_0 = \frac{e^2}{2\alpha hc}\]
**Definition 1.2.18 ** The **vacuum permeability** $\mu_0$ is the physical constant defined in terms of the fine structure constant $\alpha$, charge of an electron $e$, Plank constant $h$ and speed of light $c$.
\[\mu_0 = \frac{2\alpha h}{e^2c}\]
**Result 1.2.19 ** The **product of vacuum permittivity and vacuum permeability** is the reciprocal of the speed of light squared.
\[\varepsilon_0\mu_0 = \frac{1}{c^2}\]
### 1.3 Maxwell's Equations
**Law 1.3.1 ** **Maxwell's Equations** are a set of coupled differential equations that form the foundations of classical electromagnetism.
\[\nabla\cdot \vec{E} = \frac{\rho}{\varepsilon_0}\]
\[\nabla\cdot \vec{B} = 0\]
\[\nabla\times\vec{E} = -\frac{\partial \vec{B}}{\partial t}\]
\[\nabla\times \vec{B} = \mu_0\left( \vec{J} + \varepsilon_0\frac{\partial \vec{E}}{\partial t} \right)\]
**Definition 1.3.2 ** The **vacuum permittivity** $\varepsilon_0$ is the physical constant defined in terms of the fine structure constant $\alpha$, charge of an electron $e$, Plank constant $h$ and speed of light $c$.
\[\varepsilon_0 = \frac{e^2}{2\alpha hc}\]
**Definition 1.3.3 ** The **vacuum permeability** $\mu_0$ is the physical constant defined in terms of the fine structure constant $\alpha$, charge of an electron $e$, Plank constant $h$ and speed of light $c$.
\[\mu_0 = \frac{2\alpha h}{e^2c}\]
**Result 1.3.4 ** The **product of vacuum permittivity and vacuum permeability** is the reciprocal of the speed of light squared.
\[\varepsilon_0\mu_0 = \frac{1}{c^2}\]
## 2 Electrostatics
### 2.1 Electric Field
**Definition 2.1.1 ** The **electric field** denoted $\vec{E}(\vec{r})$ is a vector field of the force that would be felt by a test charge at a point in space. The units of electric field are Newtons per Coulomb denoted $N/C$. For a charge $q$ at position $\vec{r}$ the force $\vec{F}$ from electric field $\vec{E}$ can be calculated with the following equation:
\[\vec{F} = q\vec{E}(\vec{r})\]
**Definition 2.1.2 ** The **electric displacement field** denoted $\vec{D}$ is defined in terms of the electric field $\vec{E}$ the polarization $\vec{P}$.
\[\vec{D} = \varepsilon_0\vec{E} + \vec{P}\]
**Definition 2.1.3 ** The **polarization** denoted $\vec{P}$ is the [electric dipole moment](https://kaedon.net/l/^ahc1#wr8f) per unit volume of the bound charge density $\rho_b$ in a material.
\[\vec{P} = \frac{d\vec{p}}{dV}\]
\[- \nabla\cdot\vec{P} = \rho_b\]
**Law 2.1.4 ** **Coulomb's law** states that the force $\vec{F}$ on a point charge $q_1$ located at $\vec{r}_1$ due to another point charge $q_2$ located at $\vec{r}_2$ can be obtained with the following equation: $\newcommand\abs[1]{\left|#1\right|}$
\[\vec{F} = \frac{1}{4\pi\varepsilon_0}q_1q_2\frac{\vec{r}_1-\vec{r}_2}{\abs{\vec{r}_1-\vec{r}_2}^3}\]
**Result 2.1.5 ** The **electric field of a point charge** $q_1$ located at $\vec{r}_1$ can be directly obtained from coulomb's law.$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{E}(\vec{r}) = \frac{1}{4\pi\varepsilon_0}q_1\frac{\vec{r}-\vec{r}_1}{\abs{\vec{r}-\vec{r}_1}^3}\]
**Result 2.1.6 ** The **electric field of many point charges** $q_1,\dots,q_n$ located at $\vec{r}_1,\dots,\vec{v}_n$ can be directly obtained from coulomb's law.$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{E}(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\sum_{i=1}^n{q_i}\frac{\vec{r}-\vec{r}_i}{\abs{\vec{r}-\vec{r}_i}^3}\]
**Definition 2.1.7 ** A **charge density** denoted $\rho(\vec{r})$ is the function whose integral represents the charge in a region of space.
**Result 2.1.8 ** The **electric field of a charge density** $\rho$ can be obtained by direct integration.$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{E}(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int{ \rho(\vec{r}') \frac{\vec{r}-\vec{r}'}{\abs{\vec{r}-\vec{r}'}^3} d^3r'}\]
**Law 2.1.9 ** **Gauss's law** states that states that the surface integral of the electric field $\vec{E}$ dotted with the normal vector $\vec{n}$ over a piecewise smooth boundary $S$ of a volume $V$ is the volume integral of the charge density $\rho$ over a volume $V$.
\[\iint_S (\vec{E}\cdot \vec{n}) d^2r = \frac{1}{\varepsilon_0}\iiint_V\rho(\vec{r})d^3r\]
**Result 2.1.10 ** **Gauss's law for discrete charges** states that for discrete charges the volume integral can be simplified into a sum of the chargest inside the volume.
\[\iint_S (\vec{E}\cdot \vec{n}) d^2r = \frac{1}{\varepsilon_0}\sum_i{q_i}\]
### 2.2 Electric Potential
**Definition 2.2.1 ** The **electric potential** or **voltage** denoted $V(\vec{r},t)$ is a scalar potential such that the negative gradient is the electric field in electrostatic systems.
\[\vec{E} = -\nabla V - \frac{\partial \vec{A}}{\partial t}\]
**Result 2.2.2 ** The **electric potential of a charge density** can be obtained by direct integration.$\newcommand\abs[1]{\left|#1\right|}$
\[V(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int{ \frac{\rho(\vec{r}')}{\abs{\vec{r}-\vec{r}'}} d^3r'}\]
**Result 2.2.3 ** The **electric fields near a surface charge distribution** are discontinuous in the direction normal $\vec{n}$ to the surface charge density $\sigma$.
\[(\vec{E}_{out}-\vec{E}_{in})\cdot\vec{n} = \sigma(\vec{r})/\varepsilon_0\]
**Result 2.2.4 ** The **electric potentials near a surface dipole layer**, with dipole moment $\vec{D}(\vec{r})$ in the direction normal to the surface, are discontinuous proportional to the dipole moment $D(\vec{r})$.
\[V_2-V_1 = D(\vec{r})/\varepsilon_0\]
**Result 2.2.5 ** The **potential energy of many point charges** $W$ is the total energy of a set of many point charges $q_1,\dots,q_n$ at positions $\vec{r}_1,\dots,\vec{r}_n$ due to the forces acting between them.$\newcommand\abs[1]{\left|#1\right|}$
\[W = \frac{1}{8\pi\varepsilon_0}\sum_i\sum_j\frac{q_iq_j}{\abs{\vec{r}_i-\vec{r}_j}}\]
**Result 2.2.6 ** The **potential energy of a charge distribution** $W$ is the total energy of a charge distribution $\rho(\vec{r})$.$\newcommand\abs[1]{\left|#1\right|}$
\[W = \frac{1}{8\pi\varepsilon_0}\int\int\frac{\rho(\vec{r})\rho(\vec{r}')}{\abs{\vec{r}-\vec{r}'}}d^3r\ d^3r' = \frac{\varepsilon_0}{2}\int\abs{\vec{E}}^2d^3r\]
### 2.3 Spherical Harmonics
**Definition 2.3.1 ** The **Legendre polynomials** $P_\ell(x)$ are a set of polynomials defined on the interval $-1\leq x \leq 1$ for $\ell \in \{0,1,2,\dots\}$ by the following expression.
\[P_\ell(x) = \frac{1}{2^\ell}\]
**Definition 2.3.2 ** The **associated Legendre polynomials** $P_\ell^m(x)$ are a set of polynomials defined on the interval $-1\leq x \leq 1$ for $\ell \in \{0,1,2,3,\dots\}$ and $m \in \{-\ell,-\ell+1,\dots,0,\dots,\ell-1,\ell\}$ by the following expression.
\[P_\ell^m(x) = \frac{(-1)^{m}}{2^\ell\ell!}(1-x^2)^{m/2}\frac{d^{\ell+m}}{dx^{\ell+m}}(x^2-1)^\ell\]
**Definition 2.3.3 ** The **spherical harmonics** $Y_{\ell,m}(\theta,\phi)$ are a set of spherical functions defined for $\ell \in \{0,1,2,3,\dots\}$ and $m \in \{-\ell,-\ell+1,\dots,0,\dots,\ell-1,\ell\}$ that forms an orthonormal bases for the set of complex spherical functions.
\[Y_{\ell,m}(\theta,\phi) = \sqrt{\frac{2\ell+1}{4\pi}\frac{(\ell-m)!}{(\ell+m)!}} P_\ell^m(\cos\theta)e^{im\phi}\]
**Result 2.3.4 ** **Properties of Spherical Harmonics:** The spherical harmonics $Y_{\ell,m}$ and $Y_{\ell, -m}$ are related by the following relation,
\[Y_{\ell,-m}(\theta,\phi) = (-1)^{m}Y_{\ell,m}^*(\theta, \phi)\]
Spherical harmonics from an orthonormal basis with the following orthogonality and normalization conditions,
\[\int_0^{2\pi}\int_0^\pi Y^*_{\ell,m'}(\theta,\phi)Y_{\ell,m}(\theta,\phi) \sin\theta\ d\theta\ d\phi = \delta_{\ell',\ell}\delta_{m',m}\]
Spherical harmonics span the set of all complex spherical functions as show by the following completeness relation,
\[\sum_{\ell = 0}^\infty \sum_{m=-\ell}^\ell Y_{\ell,m}^*(\theta',\phi')Y_{\ell,m}(\theta,\phi) = \delta(\phi-\phi')\delta(\cos\theta-\cos\theta')\]
**Table 2.3.5 ** **Table of Spherical Harmoincs**
\[Y_{0,0} = \frac{1}{\sqrt{4\pi}}\]
\[Y_{1,1} = -\sqrt{\frac{3}{8\pi}}\sin\theta\ e^{i\phi}\]
\[Y_{1,0} = \sqrt{\frac{3}{4\pi}}\cos\theta\]
\[Y_{2,2} = \frac{1}{4}\sqrt{\frac{15}{2\pi}} \sin^2\theta\ e^{2i\phi}\]
\[Y_{2,1} = -\sqrt{\frac{15}{8\pi}}\sin\theta\cos\theta\ e^{i\phi}\]
\[Y_{2,0} = \sqrt{\frac{5}{4\pi}}\left(\frac{3}{2}\cos^2\theta - \frac{1}{2}\right)\]
### 2.4 Electric Multipole Expansion
**Theorem 2.4.1 ** The **multipole expansion theorem** states that for a charge distribution localized within a sphere, the electric potential outside the sphere can be written in terms of spherical harmonics.
\[V(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\sum_{\ell=0}^\infty\sum_{m=-\ell}^\ell\frac{4\pi}{2\ell+1}q_{\ell,m}\frac{Y_{\ell,m}(\theta,\phi)}{r^{\ell+1}}\]
\[q_{\ell,m} = \int Y^*_{\ell,m}(\theta,\phi)r^{\ell}\rho(\vec{r})d^3r\]
**Result 2.4.2 ** The multipole moment $q_{\ell,m}$ and $q_{\ell, -m}$ are related by the relation $q_{\ell,-m} = (-1)^{m}q^*_{\ell,m}$.
**Definition 2.4.3 ** The **monopole moment** $q$ of a charge distribution $\rho(\vec{r})$ is simply the total charge.
\[q = \int \rho(\vec{r}) d^3r\]
**Definition 2.4.4 ** The **dipole moment** $\vec{p}$ of a charge distribution $\rho(\vec{r})$ is defined with the following integral.
\[\vec{p} = \int\vec{r}\rho(\vec{r})d^3r\]
**Definition 2.4.5 ** The **quadrupole moment** $Q$ of a charge distribution $\rho(\vec{r})$ is a $3$ by $3$ matrix with components $Q_{j,k}$ defined with the following integral.
\[Q_{j,k} = \int \left[3r_jr_k-r^2\delta_{j,k}\right]\rho(\vec{r})d^3r\]
**Result 2.4.6 ** The multipole expansion of a charge distribution can be written in terms of the multiple moments of the charge distribution. The first 6 terms of the multiple expansion are written below in terms of the monopole moment $q$, the dipole moment $\vec{p}$ and the quadrupole moment $Q$ of a charge distribution $\rho(\vec{r})$.
\[q_{0,0} = \frac{1}{\sqrt{4\pi}}\int\rho(\vec{r})d^3r = \frac{1}{\sqrt{4\pi}}q\]
\[q_{1,1} = -\sqrt{\frac{3}{8\pi}}\int(x-iy)\rho(\vec{r})d^3r = -\sqrt{\frac{3}{8\pi}}(p_x-ip_y)\]
\[q_{1,0} = \sqrt{\frac{3}{4\pi}}\int z\rho(\vec{r})d^3r = \sqrt{\frac{3}{4\pi}}p_z\]
\[q_{2,2} = \frac{1}{4}\sqrt{\frac{15}{2\pi}}\int(x-iy)\rho(\vec{r})d^3r = \frac{1}{12}\sqrt{\frac{15}{2\pi}}(Q_{1,1}-2iQ_{1,2}-Q_{2,2})\]
\[q_{2,1} = -\sqrt{\frac{15}{8\pi}}\int z(x-iy)\rho(\vec{r})d^3r = -\frac{1}{3}\sqrt{\frac{15}{8\pi}}(Q_{1,3}-iQ_{2,3})\]
\[q_{2,0} = \frac{1}{2}\sqrt{\frac{5}{4\pi}}\int(3z^2-r^2)\rho(\vec{r})d^3r = \frac{1}{2}\sqrt{\frac{5}{4\pi}}Q_{3,3}\]
### 2.5 Cartesian Separation of Variables
**Theorem 2.5.1 ** The solution $y(x)$ to a **second order linear differential equation** of the form
\[a\frac{d^2 y(x)}{dx^2} + b\frac{d y(x)}{dx} + c y(x) = 0\]
is $y=Ae^{r_1x} + Be^{r_2x}$ for some constants $A,B\in\mathbb{C}$ and where $r_1,r_2\in\mathbb{C}$ are the two solutions to the quadratic equation $ar^2 + br + c = 0$.
**Corollary 2.5.2 ** An equation of the form $\frac{1}{y(x)}\frac{d^2 y(x)}{dx^2} = k$ has solution $y(x) = Ae^{\sqrt{k}x} + Be^{-\sqrt{k}x}$ for some constants $A,B\in\mathbb{C}$.
**Definition 2.5.3 ** **Separation of variables** is a technique solve differential equations by algebraically separating the equation into independent one dimensional differential equations.
**Definition 2.5.4 ** The **Laplace equation** is for a scalar function $V(\vec{r})$ is the second-order partial differential equation defined by
\[\nabla^2V(\vec{r}) = 0\]
where $\nabla^2$ is the [Laplace operator](https://kaedon.net/l/^pd4j#59d9). This equation describes how an electrostatic potential function behaves in a region with zero charge density.
**Theorem 2.5.5 ** The **uniqueness theorem for the Laplace equation** states that for a
**Result 2.5.6 ** The **Laplace equation written in Cartesian coordinates** for a potential $V(x,y,z)$ is
\[\nabla^2 V(\vec{r}) = \frac{\partial^2 V(\vec{r})}{\partial x^2} + \frac{\partial^2 V(\vec{r})}{\partial y^2} + \frac{\partial^2 V(\vec{r})}{\partial z^2} = 0\]
**Result 2.5.7 ** Applying **separation of variables for the Laplace equation in Cartesian coordinates** and assuming that the solution is in product form $V(x,y,z) = X(x)Y(y)Z(z)$, produces the following differential equations.
\[\frac{1}{X}\frac{d^2 X}{d x^2} + \frac{1}{Y}\frac{d^2 Y}{d y^2} + \frac{1}{Z}\frac{d^2 Z}{d z^2} = 0\]
\[\frac{1}{X}\frac{d^2 X}{d x^2} = k_x,\quad \frac{1}{Y}\frac{d^2 Y}{d y^2} = k_y,\quad \frac{1}{Z}\frac{d^2 Z}{d z^2} = k_z\]
### 2.6 Spherical Separation of Variables
**Result 2.6.1 ** The **Laplace equation in spherical coordinates** for a potential $V(r,\theta,\phi)$ is
\[\frac{1}{r}\frac{\partial^2}{\partial r^2}(rV(\vec{r})) + \frac{1}{r^2\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\ \frac{\partial V(\vec{r})}{\partial \theta}\right) + \frac{1}{r^2\sin^2\theta} \frac{\partial^2V(\vec{r})}{\partial \phi} = 0\]
**Result 2.6.2 ** Applying **separation of variables for the Laplace equation in Spherical coordinates** and assuming that the solution is in product form $V(r,\theta,\phi) = \frac{U(r)}{r}P(\theta)Q(\phi)$, produces the following differential equation.
\[r^2\sin^2\theta\left[ \frac{1}{U}\frac{d^2 U}{dr^2} + \frac{1}{Pr^2\sin\theta}\frac{d}{d\theta}\left(\sin\theta\ \frac{dP}{d\theta}\right) \right] + \frac{1}{Q}\frac{d^2Q}{d\phi^2} = 0\]
From this it can be shown that any solution can be written in terms of spherical harmonics with coefficients $A_{\ell,m},B_{\ell,m}\in\mathbb{R}$.
\[V(r,\theta,\phi) = \sum_{\ell=0}^\infty{\sum_{m=-\ell}^\ell{\left[ A_{\ell,m} r^\ell + \frac{B_{\ell,m}}{r^{\ell+1}} \right]Y_{\ell,m}(\theta,\phi)}}\]
\[A_{\ell,m}a^{\ell} + \frac{B_{\ell,m}}{a^{\ell+1}} = \int Y^*_{\ell,m}(\theta,\phi)V(r=a,\theta,\phi)d\Omega\]
**Corollary 2.6.3 ** A **Legendre polynomial solution to the Laplace equation in spherical coordinates** for systems with azimuthal symmetry can be written in terms of [Legendre polynomials](https://kaedon.net/l/^ahc1#85ep) $P_\ell$ with coefficients $A_{\ell,m},B_{\ell,m}\in\mathbb{R}$.
\[V(r,\theta) = \sum_{\ell = 0}^\infty\left[A_{\ell,m} r^\ell + \frac{B_{\ell,m}}{r^{\ell+1}}\right]P_\ell(\cos\theta)\]
### 2.7 Cylindrical Separation of Variables
**Result 2.7.1 ** The **Laplace equation in cylindrical coordinates** for a potential $V(s,\phi,z)$ is
\[\frac{\partial^2 V(\vec{r})}{\partial s^2} + \frac{1}{s}\frac{\partial V(\vec{r})}{\partial s} + \frac{1}{s^2}\frac{\partial^2 V(\vec{r})}{d\phi^2} + \frac{\partial^2 V(\vec{r})}{\partial z^2} = 0\]
**Result 2.7.2 ** Applying **separation of variables for the Laplace equation in cylindrical coordinates** and assuming that the solution is in product form $V(s,\phi,z) = S(s)Q(\phi)Z(z)$, produces the following system of differential equations for some constants $k,v\in\mathbb{R}$.
\[\frac{1}{Z(z)}\frac{\partial^2 Z(z)}{\partial z^2} = k^2\]
\[\frac{1}{Q(\phi)}\frac{\partial^2 Q(\phi)}{\partial \phi^2} = -v^2\]
\[\frac{\partial^2 S(s)}{\partial s^2} + \frac{1}{s}\frac{\partial S(s)}{\partial s} + \left(k^2 - \frac{v^2}{s^2}\right)S(s) = 0\]
**Definition 2.7.3 ** The **Bessel functions** are the canonical solutions $y(x)$ of **Bessel's differential equation**, defined below for some complex number $\alpha$.
\[x^2\frac{d^2y}{dx^2} + x\frac{dy}{dx} + (x^2 - \alpha^2)y = 0\]
**Corollary 2.7.4 ** The third differential equation in separation of variables for the Laplace equation in cylindrical coordinates can be written as Bessel's differential equation where $x=ks$ and $\alpha = v$,
\[x^2\frac{d^2y}{dx^2} + x\frac{dy}{dx} + (x^2 - v^2)y = 0\]
\[\frac{d^2y}{dx^2} + \frac{1}{x}\frac{dy}{dx} + \left(1 - \frac{v^2}{x^2}\right)y = 0\]
**Definition 2.7.5 ** The **Bessel functions of the first kind** denoted $J_\alpha(x)$ are solutions of Bessel's differential equation for $\alpha\in\mathbb{C}$ defined by the following equation where $\Gamma$ is the gamma function.
\[J_{\alpha}(x) = \sum_{n=0}^\infty\frac{(-1)^n}{n!\Gamma(n+\alpha+1)}\left(\frac{x}{2}\right)^{2n+\alpha}\]
**Definition 2.7.6 ** The **Bessel functions of the second kind** or **Neumann functions** denoted $N_\alpha(x)$ are solutions of Bessel's differential equation for $\alpha\in\mathbb{C}$ defined by the following equation where $J_\alpha$ are the Bessel functions of the first kind.
\[N_\alpha(x) = \frac{J_\alpha(x)\cos(\alpha\pi) - J_{-\alpha}(x)}{\sin(\alpha\pi)}\]
**Definition 2.7.7 ** The **Bessel functions of the third kind** or **Hankel functions** denoted $H_\alpha^{(1)}(x),H_\alpha^{(2)}(x)$ are solutions of Bessel's differential equation for $\alpha\in\mathbb{C}$ defined by the following equation where $J_\alpha$ and $N_{\alpha}$ are Bessel functions of the first and second kind respectively.
\[H_\alpha^{(1)}(x) = J_\alpha(x) + i N_\alpha(x)\]
\[H_\alpha^{(2)}(x) = J_\alpha(x) - i N_\alpha(x)\]
### 2.8 Method of Relaxation
**Definition 2.8.1 ** The **method of relaxation** is a numerical method for solving the Laplace equation for a finite region of space with known boundary conditions iteratively. This method computes the potential $V(\vec{r})$ at a finite number of point by iteratively setting each point to the average of the points around it.
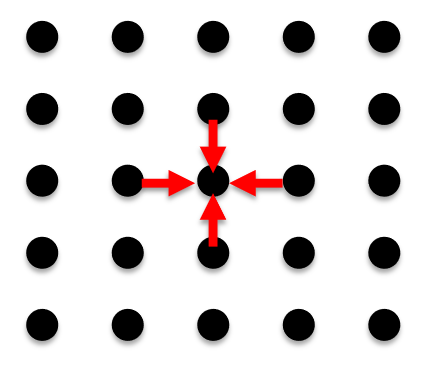 **File 2.8.2 ** Relaxation.PNG
### 2.9 Finite Element Method
**Definition 2.9.1 ** The **finite element method** is a computational method for calculating an approximation of the solution to a differential equation with a finite mesh to represent the geometry of the system.
### 2.10 Green's Function Theory
**Definition 2.10.1 ** A **linear differential operator** is a functional operator involving differentiation that is [linear](https://kaedon.net/l/^n96p).
**Definition 2.10.2 ** The **Green's function** denoted $G$ for a linear operator $\mathcal{L}$ is the solution to the following equation where $\delta$ is the [Dirac delta](https://kaedon.net/l/^wna1).
\[\mathcal{L}G(\vec{r},\vec{r}')=-4\pi\delta(\vec{r}-\vec{r}')\]
**Corollary 2.10.3 ** Let $G(\vec{r},\vec{r}')$ be a [Green's function](https://kaedon.net/l/^1mfe) for a [linear differential operator](https://kaedon.net/l/^3r0m) $\mathcal{L}$ and $F(\vec{r},\vec{r}')$ be any function such that $\mathcal{L}F=0$, then the function $G'(\vec{r},\vec{r}')$ defined below is also a Green's function for $\mathcal{L}$.
\[G'(\vec{r},\vec{r}') = G(\vec{r},\vec{r}') + F(\vec{r},\vec{r}')\]
**Definition 2.10.4 ** The **differential form for Green's function theory** is the following differential form solving for $u(\vec{r})$ where $\mathcal{L}$ is a linear differential operator and $f(\vec{r})$ is an arbitrary distribution.
\[\mathcal{L}u(\vec{r})=f(\vec{r})\]
**Theorem 2.10.5 ** The solution to a differential equation of the [form](https://kaedon.net/l/^fh5f) $\mathcal{L}u(\vec{r})=f(\vec{r})$ is the integral of the [Green's function](https://kaedon.net/l/^1mfe) $G$ of the [linear differential operator](https://kaedon.net/l/3r0m) $\mathcal{L}$ and the distribution $f(\vec{r})$.
\[u(\vec{r}) = -\frac{1}{4\pi}\int{ f(\vec{r}')G(\vec{r},\vec{r}') d^3r'}\]
**Result 2.10.6 ** A **[Green's function](https://kaedon.net/l/^1mfe) for the [Laplace operator](https://kaedon.net/l/^59d9)** $G(\vec{r},\vec{r}')$ is the following function. $\newcommand\abs[1]{\left|#1\right|}$
\[G(\vec{r},\vec{r}') = \frac{1}{\abs{\vec{r}-\vec{r}'}}\]
**Result 2.10.7 ** The **electric potential of a charge density** can be obtained by direct integration.$\newcommand\abs[1]{\left|#1\right|}$
\[V(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int{ \frac{\rho(\vec{r}')}{\abs{\vec{r}-\vec{r}'}} d^3r'}\]
**Theorem 2.10.8 ** The solution to a differential equation of the form $\mathcal{L}u(\vec{r}) = f(\vec{r})$ in the volume $V$ with boundary conditions on surface $S$ is the sum of the following integrals of a [Green's function](https://kaedon.net/l/1mfe) $G$ of the linear differential operator $\mathcal{L}$ and the arbitrary function $f(\vec{r})$, where $\hat{n}$ is the normal vector of the surface $S$ pointing outward from the volume $V$.
\[u(\vec{r}) = -\frac{1}{4\pi}\int_{V}{ f(\vec{r}')G(\vec{r},\vec{r}') d^3r'} + \frac{1}{4\pi}\oint_S\left[\frac{\partial u(\vec{r}')}{\partial n'}\right]G(\vec{r},\vec{r}')d^2r' - \frac{1}{4\pi}\oint_S\left[u(\vec{r}')\right]\frac{\partial G(\vec{r},\vec{r}')}{\partial n'}d^2r'\]
**Result 2.10.9 ** The **electric potential of the charge distribution with boundary conditions** can be obtain by direct integration with an appropriate choice of [Green's function](https://kaedon.net/l/1mfe) $G$ for the Laplace operator $\nabla^2$. Let $A$ be the volume of interest, $S$ be the boundary surface of $A$ and $\rho(\vec{r})$ be the charge density inside the volume $A$. The electric potential is determined by the following integrals of Green's functions.
\[V(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int_{A}{ \rho(\vec{r}')G(\vec{r},\vec{r}') d^3r'} + \frac{1}{4\pi}\oint_S\left[\frac{\partial V(\vec{r}')}{\partial n'}\right]G(\vec{r},\vec{r}')d^2r' - \frac{1}{4\pi}\oint_S\left[V(\vec{r}')\right]\frac{\partial G(\vec{r},\vec{r}')}{\partial n'}d^2r'\]
**Definition 2.10.10 ** The **Dirichlet condition** is the boundary condition where the potential $V(\vec{r})$ on the bounding surface is known.
**Definition 2.10.11 ** The **Neumann condition** is the boundary condition where the normal derivative of the potential $\frac{\partial V(\vec{r})}{\partial n}$ on the bounding surface is known.
**Result 2.10.12 ** The **electric potential $V(\vec{r})$ caused by a sphere with known potential** can be calculated with integrals of the following [Green's Function](https://kaedon.net/l/^ahc1#1mfe) $G(\vec{r},\vec{r}')$ for the volume $A$ inside or outside a sphere of radius $R$ centered at the origin with bounding surface $S$, where $\hat{n}$ is the normal vector of the surface $S$ pointing outward from the volume $V$.
\[G(\vec{r},\vec{r}') = \frac{1}{\abs{\vec{r}-\vec{r}'}} - \frac{\frac{R}{r'}}{\abs{\vec{r}-\frac{R^2}{r'^2}\vec{r}'}}\]
\[\left.\frac{\partial G(\vec{r},\vec{r}')}{\partial n'}\right|_{r'=R} = \frac{-\abs{r^2 - R^2}}{R\left(r^2+R^2-2Rr\left[\cos\theta\cos\theta'+\sin\theta\sin\theta'\cos(\phi-\phi')\right]\right)^{3/2}}\]
\[V(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int_{A}{ \rho(\vec{r}')G(\vec{r},\vec{r}') d^3r'} - \frac{1}{4\pi}\oint_S\left[V(\vec{r}')\right]\frac{\partial G(\vec{r},\vec{r}')}{\partial n'}d^2r'\]
## 3 Magnetostatics
### 3.1 Magnetic Field
**Definition 3.1.1 ** The **magnetic field** or **magnetic flux density** denoted $\vec{B}$ is the vector field that describes the force per length of current in a region of space. This is the actual magnetic field at a point in space.
**Definition 3.1.2 ** The **magnetic field strength** denoted $\vec{H}$ is the vector that described the external contribution to the magnetic field in a material not intrinsic to the material's magnetization $\vec{M}$, where $\mu_0$ is the vacuum permeability.
\[\vec{H} = \frac{\vec{B}}{\mu_0} - \vec{M}\]
**Definition 3.1.3 ** A **surface current density** denoted $\vec{K}(\vec{r})$ is a vector field describing the density of current flowing on a surface.
**Result 3.1.4 ** The current $I$ crossing a line $L$ on a surface $S$ with surface current density $\vec{K}(\vec{r})$ is given by the following path integral relative to a unit vector $\hat{n}$ pointing from the origin to each point on the line.
\[I = \int_L (\vec{K}\times\hat{n})\cdot d\vec{L}\]
**Definition 3.1.5 ** A **volume current density** denoted $\vec{J}(\vec{r})$ is a vector field describing the density of current flowing at a particular point in space.
**Result 3.1.6 ** The current $I$ passing through a surface $S$ in a space with volume current density $\vec{J}(\vec{r})$ is given by the following surface integral.
\[I = \int_S \vec{J}\times d\vec{S}\]
**Law 3.1.7 ** The **Biot-Savart law** states that the magnetic field $\vec{B}$ produced by a current carrying wire, a surface current density $\vec{K}(\vec{r}')$ or a volume current density $\vec{J}(\vec{r})$ in a vacuum is determined by the following integrals.$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{B} = \frac{\mu_0I}{4\pi}\int_L\frac{d\vec{r}'\times\left(\vec{r}-\vec{r}'\right)}{\abs{\vec{r}-\vec{r}'}^3}\]
\[\vec{B} = \frac{\mu_0}{4\pi}\int_S\frac{\vec{K}(\vec{r}')\times(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^2\vec{r}'\]
\[\vec{B} = \frac{\mu_0}{4\pi}\int_V\frac{\vec{J}(\vec{r}')\times(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3\vec{r}'\]
**Law 3.1.8 ** **Ampere's circuit law** states that the loop integral of the magnetic field along a loop $C$ is equal to the surface integral of the current flux out of a surface $S$ bounded by $C$. This is a consequence of [Stoke's theorem](https://kaedon.net/l/7ahh) and [Maxwell's equations](https://kaedon.net/l/3a2h).
\[\oint_C\vec{B}\cdot d\vec{\ell} = \mu_0\int_S\vec{J}\cdot d\vec{S} = \mu_0I_{\text{enclosed}}\]
**Result 3.1.9 ** The **force $\vec{F}$ on a current carrying wire** with current $I$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following path integral:
\[\vec{F} = I\int{d\vec{\ell}\times \vec{B}(\vec{r}')}\]
**Result 3.1.10 ** The **torque $\vec{N}$ on a current density $\vec{J}(\vec{r})$** around a pivot point $\vec{r}_p$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following integral:
\[\vec{N}(\vec{r}_p) = \int \left[\vec{r}' - \vec{r}_p'\right]\times \left[\vec{J}(\vec{r}')\times\vec{B}(\vec{r}')\right]d^3r'\]
### 3.2 Magnetic Forces
**Law 3.2.1 ** The **Lorentz force law** states that the force $\vec{F}$ on a charged particle with charge $q$ moving at velocity $\vec{v}$ through magnetic field $\vec{B}$ is determined by the following cross product.
\[\vec{F} = q\vec{v}\times\vec{B}\]
**Result 3.2.2 ** The **force $\vec{F}$ on a current density $\vec{J}(\vec{r})$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following integral:
\[\vec{F} = \int{\vec{J}(\vec{r}')\times\vec{B}(\vec{r}')d^3r'}\]
**Result 3.2.3 ** The **force $\vec{F}$ on a current carrying wire** with current $I$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following path integral:
\[\vec{F} = I\int{d\vec{\ell}\times \vec{B}(\vec{r}')}\]
**Result 3.2.4 ** The **torque $\vec{N}$ on a current density $\vec{J}(\vec{r})$** around a pivot point $\vec{r}_p$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following integral:
\[\vec{N}(\vec{r}_p) = \int \left[\vec{r}' - \vec{r}_p'\right]\times \left[\vec{J}(\vec{r}')\times\vec{B}(\vec{r}')\right]d^3r'\]
**Result 3.2.5 ** The **torque $\vec{N}$ on a current carrying wire** with current $I$ around a pivot point $\vec{r}_p$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following path integral:
\[\vec{N}(\vec{r}_p) = I \int \left[\vec{r}' - \vec{r}_p'\right]\times \left[d\vec{\ell}'\times\vec{B}(\vec{r}')\right]\]
### 3.3 Magnetic Potential
**Definition 3.3.1 ** The **magnetic potential** denoted $\vec{A}(\vec{r},t)$ is a vector potential such that the curl of the potential is the magnetic field.
\[\vec{B} = \nabla \times \vec{A}\]
**Definition 3.3.2 ** A **gauge** is a any choice of configuration of the unobservable fields that does not affect the observable fields.
**Definition 3.3.3 ** A **gauge transformation** is any transformation of the unobservable fields that does not affect the observable fields.
**Result 3.3.4 ** Any **arbitrary gauge transformation** acting on magnetic potential $\vec{A}(\vec{r},t)$ and electric potential $V(\vec{r},t)$ takes the following form for some scalar field $\Psi(\vec{r},t)$.
\[\vec{A}\to \vec{A} + \nabla\Psi\]
\[V \to V - \frac{\partial \Psi}{\partial t}\]
**Definition 3.3.5 ** The **Coulomb gauge** is the convention that $\nabla\cdot\vec{A} = 0$.
**Result 3.3.6 ** The **magnetic potential in the Coulomb gauge** can be directly integrated from the volume current density $\vec{J}$ or the magnetic field $\vec{B}$ with one of the following integrals.$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{A}(\vec{r}) = \frac{\mu_0}{4\pi}\int\frac{\vec{J}(\vec{r}')}{\abs{\vec{r}-\vec{r}'}}d^3r'\]
\[\vec{A}(\vec{r}) = \frac{1}{4\pi}\int\frac{\vec{B}(\vec{r}')\times(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
### 3.4 Magnetic Dipole Moment
**Definition 3.4.1 ** The **magnetic dipole moment** denoted $\vec{m}$ of a current density $\vec{J}(\vec{r})$ is defined with the following integral.
\[\vec{m} = \frac{1}{2}\int\vec{r}'\times\vec{J}(\vec{r}')d^3\vec{r}'\]
**Result 3.4.2 ** The **magnetic potential $\vec{A}$ of a magnetic dipole moment** $\vec{m}$ is given by the following formula.
\[\vec{A} = \frac{\mu_0}{4\pi} \frac{\vec{m}\times\vec{r}}{r^3}\]
**Result 3.4.3 ** The **magnetic field $\vec{B}$ of a magnetic dipole moment** $\vec{m}$ is given by the following formula where $\newcommand\abs[1]{\left|#1\right|}\hat{n} = \frac{\vec{r}-\vec{r}_m}{\abs{\vec{r}-\vec{r}_m}}$ is the unit vector pointing from the position of the magnetic dipole moment $\vec{r}_m$ and the observation point $\vec{r}$.
\[\vec{B}(\vec{r}) = \frac{\mu_0}{4\pi}\left[\frac{3\hat{n}\left(\hat{n}\cdot\vec{m}\right) - \vec{m}}{\abs{\vec{r}-\vec{r}_m}^3} + \frac{8\pi}{3}\vec{m}\delta^3(\vec{r}-\vec{r}_m)\right]\]
**Result 3.4.4 ** The **force $F$ on a magnetic dipole moment** $\vec{m}$ in a magnetic field $\vec{B}$ is given by the following dot product gradient.
\[\vec{F} = \nabla\left( \vec{m}\cdot\vec{B} \right)\]
**Result 3.4.5 ** The **torque $\vec{\tau}$ on a magnetic dipole moment** $\vec{m}$ in a magnetic field $\vec{B}$ is given by the following cross product.
\[\vec{\tau} = \vec{m}\times\vec{B}\]
### 3.5 Magnetic Quadrupole Field
**Definition 3.5.1 ** The **magnetic quadrupole field** is the magnetic field produced by four infinitely lone wire run parallel to the z-axis with currents $-I\hat{z}$ at $(0,\pm R,0)$ and $+I\hat{z}$ at $(\pm R,0,0)$.
\[\vec{B} = -\frac{2\mu_0 I}{\pi R} \left[\frac{y\hat{x}+x\hat{y}}{R}\right]\]
## 4 Special Relativity
### 4.1 Lorentz Transformations
**Definition 4.1.1 ** An **inertial reference frame** is a coordinate system that moves with a constant rectilinear velocity.
**Definition 4.1.2 ** The **simultaneity beta** denoted $\vec{\beta}$ is the vector $\vec{\beta} = \frac{\vec{v}}{c}$ where $v$ is the velocity of a reference frame and $c$ is the speed of light.
**Definition 4.1.3 ** The **simultaneity gamma** denoted $\gamma$ is the scalar $\gamma = \left(1-\beta^2\right)^{-1/2}$, where $\newcommand\abs[1]{\left|#1\right|}\beta=\abs{\vec{\beta}}$ is [simultaneity beta](https://kaedon.net/l/^ahc1#awac).
**Definition 4.1.4 ** A **Lorentz transformation** is a transformation $\Lambda:\mathbb{R}^{1,3}\to\mathbb{R}^{1,3}$ the preserves the scalar $(A_0-B_0)^2-(A_1-B_1)^2-(A_2-B_2)^2-(A_3-B_3)^2$ for all $A,B\in\mathbb{R}^{1,3}$.
**Definition 4.1.5 ** The **Poincaré group** or the **inhomogeneous Lorentz group** is the group of all [Lorentz transformations](https://kaedon.net/l/^ahc1#7823) such as translations, rotations and boosts.
**Definition 4.1.6 ** A **homogeneous Lorentz transformation** is a transformation $\Lambda:\mathbb{R}^{1,3}\to\mathbb{R}^{1,3}$ that preserves the scalar $A_0^2-A_1^2-A_2^2-A_3^2$ for all $A\in\mathbb{R}^{1,3}$.
**Definition 4.1.7 ** The **homogeneous Lorentz group** or sometimes simply the **Lorentz group** is the group of all [homogeneous Lorentz transformations](https://kaedon.net/l/^ahc1#59kr). This only includes linear transformations such as rotations and boosts, but not non-linear transformations such as translations.
**Proposition 4.1.8 ** [Homogeneous Lorentz transformations](https://kaedon.net/l/^ahc1#59kr) are [Lorentz transformations](https://kaedon.net/l/^ahc1#7823).
**Definition 4.1.9 ** The **Lortenz boost** $A\mapsto A'$ is a [homogeneous Lorentz transformation](https://kaedon.net/l/^ahc1#59kr) that transforms any [four vector](https://kaedon.net/l/^ahc1#m43n) $A\in\mathbb{R}^{1,3}$ to a four vector in a reference frame moving with relative velocity $\vec{v}$ and [simultaneity beta](https://kaedon.net/l/^ahc1#awac) $\vec\beta = \frac{\vec{v}}{c}$.
\[A_0' = \gamma(A_0 - \vec{\beta}\cdot\vec{A})\]
\[\vec{A}' = \vec{A}+\frac{(\gamma - 1)}{\beta^2}(\vec{\beta}\cdot\vec{A})\vec{\beta}-\gamma\vec{\beta}A_0\]
**Result 4.1.10 ** The [Lorentz boost](https://kaedon.net/l/^ahc1#5zte) $A\mapsto A'$ into a frame with relative velocity $\vec{v}$ and [simultaneity beta](https://kaedon.net/l/^ahc1#awac) $\vec\beta = \frac{\vec{v}}{c}$ can be written in terms of the component $A_\parallel$ of $A$ parallel to $\vec{\beta}$ and the component $A_\perp$ of $A$ perpendicular to $\vec{\beta}$ for $\gamma = \left(1-\beta^2\right)^{-1/2}$.
\[A'_0 = \gamma(A_0 - \vec{\beta}\cdot\vec{A})\]
\[A'_\parallel = \gamma(A_\parallel - \beta A_0)\]
\[\vec{A}'_{\perp} = \vec{A}'_\perp\]
**Result 4.1.11 ** The following **Lorentz boost matrix** $\Lambda(\vec{\beta})$ can be used to apply a [Lorentz boost](https://kaedon.net/l/^ahc1#5zte) $A\mapsto A'=\Lambda(\vec{\beta}) A$ to a four vector $A\in\mathbb{R}^{1,3}$ into a reference frame with relative velocity $\vec{v}$ and [simultaneity beta](https://kaedon.net/l/^ahc1#awac) $\vec\beta = \frac{\vec{v}}{c}$.
\[\Lambda(\vec{\beta}) = \begin{pmatrix} \gamma & -\gamma\beta_x & -\gamma\beta_y & -\gamma\beta_z \\
-\gamma\beta_x & 1+\frac{(\gamma-1)\beta_x^2}{\beta^2} & \frac{(\gamma-1\beta_x\beta_y)}{\beta^2} & \frac{(\gamma-1\beta_x\beta_z)}{\beta^2}\\
-\gamma\beta_y & \frac{(\gamma-1\beta_x\beta_y)}{\beta^2} & 1+\frac{(\gamma-1)\beta_y^2}{\beta^2} & \frac{(\gamma-1\beta_y\beta_z)}{\beta^2}\\
-\gamma\beta_z & \frac{(\gamma-1\beta_x\beta_z)}{\beta^2} & \frac{(\gamma-1\beta_y\beta_z)}{\beta^2} & 1+\frac{(\gamma-1)\beta_z^2}{\beta^2} \end{pmatrix}\]
### 4.2 Four Vectors
**Definition 4.2.1 ** A **four vector** is a vector $A=(A_0,\vec{A})\in\mathbb{R}^{1,3}$ of a time-like scalar component $A_0$ and a space-like vector component $\vec{A}=(A_1,A_2,A_3)$ where the quantity $A_0^2 -A_1^2 -A_2^2 -A_3^2$ is invariant for all reference frames and [homogeneous Lorentz transformations](https://kaedon.net/l/^ahc1#59kr).
**Definition 4.2.2 ** The **flat negative trace metric tensor** is the metric tensor that describes flat space for special relativity with the negative trace convention.
\[\eta = \begin{pmatrix}1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1\end{pmatrix}\]
**Definition 4.2.3 ** The **four vector dot product** for two four vectors $A,B\in\mathbb{R}^{1,3}$ is defined in terms of a metric tensor $\eta$.
\[A\cdot B = A^\top\eta B\]
**Definition 4.2.4 ** The **four vector norm** $\newcommand\abs[1]{\left|#1\right|}\abs{A}$ of a four vector $A\in\mathbb{R}^{1,3}$ is defined $\abs{A}=\sqrt{A\cdot A}$.
**Result 4.2.5 ** The dot product of any two four vectors is invariant under [Lorentz transformation](https://kaedon.net/l/^ahc1#59kr).
**Definition 4.2.6 ** The **4-position** is the four vector $(ct,\vec{r})$ with corresponding invariant **spacetime interval** $s^2=(ct)^2 - \abs{\vec{r}}^2$ where $c$ is the speed of light, $t$ is time and $\vec{r}$ is the position of a space-time coordinate.
**Definition 4.2.7 ** The **4-velocity** is the four vector $(\gamma_vc,\gamma_v\vec{v})$ with corresponding invariant $(\gamma_vc)^2 - \gamma_v^2\abs{\vec{v}}^2$, where $\gamma_v=\left(1-v^2/c^2\right)^{-1/2}$, $c$ is the speed of light and $\vec{v}$ is the velocity.
**Result 4.2.8 ** The **velocity addition law** describes how to combine the velocities of two objects in a way that is consistent with relativity.
**Definition 4.2.9 ** The **4-momentum** is the four vector $(E/c,\vec{p})$ with corresponding invariant $(E/c)^2 - \abs{\vec{p}}^2 = m^2c^2$ where $c$ is the speed of light, $m$ is the rest mass, $E$ is the energy and $\vec{p}$ is the momentum.
**Definition 4.2.10 ** The **4-current density** is the four vector $\left(c\rho,\vec{J}\right)$ with corresponding invariant $(c\rho)^2 - \abs{\vec{J}}^2$ where $c$ is the speed of light, $\rho$ is the charge density and $\vec{J}$ is the current density.
**Definition 4.2.11 ** The **4-wave vector** is the four vector $(\omega/c,\vec{k})$ with corresponding invariant $(\omega/c)^2 - \abs{\vec{k}}^2 = (mc/\hbar)^2$ where $c$ is the speed of light, $\omega$ is the frequency in radians per second, $\vec{k}$ is the wave vector and $m$ is the rest mass.
**Result 4.2.12 ** The phase of a wave $\phi = \omega t - \vec{k}\cdot\vec{r}$ is invariant under [Lorentz transformation](https://kaedon.net/l/^ahc1#59kr).
\[(ct,\vec{r})\cdot(\omega/c,\vec{k}) = \omega-\vec{k}\cdot\vec{r} = \phi\]
**Table 4.2.13 ** Four vectors and their corresponding invariants.$\newcommand\abs[1]{\left|#1\right|}$
| Four Vector | | Invarient | |
|:----------------|:---------|:-----------|:----------|
| 4-Position | $(ct,\vec{r})$ | Spacetime interval | $(ct)^2 - \abs{\vec{r}}^2 = s^2$ |
| 4-Velocity| $(\gamma_vc,\gamma_v\vec{v})$ | (no name) | $(\gamma_vc)^2 - \gamma_v^2\abs{\vec{v}}^2$ |
| 4-Momentum | $(E/c,\vec{p})$ | Rest mass squared | $(E/c)^2 - \abs{\vec{p}}^2 = m^2c^2$ |
| 4-Current Density | $\left(c\rho,\vec{J}\right)$ | (no name) | $(c\rho)^2 - \abs{\vec{J}}^2$ |
| 4-Wave Vector | $(\omega/c,\vec{k})$ | Rest mass over hbar squared | $(\omega/c)^2 - \abs{\vec{k}}^2 = (mc/\hbar)^2$ |
### 4.3 Einstein Notation
**Definition 4.3.1 ** **Einstein notation** or **Einstein summation notation** is a notational convention that used subscripts and superscripts to simplify summation notation over the implied range of that index. Paired indexes are summed over and unpaired indexes represent the components of the vector or tensor.
\[c_ix^i = \sum_{i=0}^3 c_ix^i = c_0x^0 + c_1x^1 + c_2x^2 + c_3x^3\]
**Definition 4.3.2 ** A **contravarient vector** is a four vector written in Einstein notation with the index in the superscript.
\[A^\mu = (A_0,\vec{A})\]
**Definition 4.3.3 ** A **covarient vector** is a four vector written in Einstein notation with the index in the subscript.
\[A_\mu = \eta_{\mu\nu}A^\nu = \sum_{\nu=0}^3\eta_{\mu\nu}A^\nu = (A_0,-\vec{A})\]
**Definition 4.3.4 ** The **scalar product** of two four vectors $a,b\in\mathbb{R}^{1,3}$ is simply the [four vector dot product](https://kaedon.net/l/^ahc1#pma4).
\[a\cdot b = a_\mu b^\mu = \eta_{\mu\nu}a^\nu b^\mu = \sum_{\mu =0}^3\sum_{\nu=0}^3\eta_{\mu\nu}a^\nu b^\mu = a_0b_0 - \vec{a}\cdot\vec{b}\]
### 4.4 Field Strength Tensor
**Definition 4.4.1 ** The **field strength tensor** $F$ is a 4-tensor that contains both the [electric field](https://kaedon.net/l/^ahc1#zf8f) and the [magnetic field](https://kaedon.net/l/^ahc1#h3d5) at a particular point in spacetime.
\[F = \begin{pmatrix} 0 & -E_x & -E_y & -E_z\\ +E_x & 0 & -B_z & +B_y \\ +E_y & +B_z & 0 & -B_x \\ +E_z & -B_y & +B_x & 0\end{pmatrix}\]
**Result 4.4.2 ** The **Lorentz boost of a 4-tensor** can be computed by applying the [Lorentz boost matrix](https://kaedon.net/l/^ahc1#059k) $\Lambda(\vec\beta)$ to a 4-tensor $T$.
\[T' = \Lambda(\vec{\beta})T\Lambda^\top\]
**Result 4.4.3 ** The **Lorentz boost of electric and magnetic fields** into a frame with relative velocity $\vec{v}$ and [simultaneity beta](https://kaedon.net/l/^ahc1#awac) $\vec\beta = \frac{\vec{v}}{c}$ can be calculated with the following formulas.
\[\vec{E}' = \gamma\left(\vec{E} + \vec\beta\times\vec{B}\right) - \frac{\gamma - 1}{\beta^2}\left(\vec\beta \cdot\vec{E}\right)\vec\beta\]
\[\vec{B}'=\gamma\left(\vec{B}-\vec\beta\times\vec{E}\right)-\frac{\gamma-1}{\beta^2}\left(\vec\beta\cdot\vec{B}\right)\vec\beta\]
**Result 4.4.4 ** The **Lorentz boost of electric and magnetic fields** into a frame with relative velocity $\vec{v}$ and [simultaneity beta](https://kaedon.net/l/^ahc1#awac) $\vec\beta = \frac{\vec{v}}{c}$ can be written in terms of the components $E_\parallel,B_\parallel$ of $E,B$ parallel to $\vec{\beta}$ and the components $E_\perp,B_\perp$ of $E,B$ perpendicular to $\vec{\beta}$.
\[\vec{E}'_\parallel = \vec{E}_\parallel\]
\[\vec{E}'_\perp = \gamma\left(\vec{E}_\perp + \vec\beta\times\vec{B}_\perp\right)\]
\[\vec{B}'_\parallel = \vec{B}_\parallel\]
\[\vec{B}'_\perp = \gamma\left(\vec{B}_\perp - \vec\beta\times\vec{E}_\perp\right)\]
**Result 4.4.5 ** The **relativistic motion in static electromagnetic fields** for a charged particle with rest mass $m$ and momentum $\vec{p}$ in electric and magnetic fields $\vec{E}$ and $\vec{B}$ the motion of this particles can be described by the following differential equation.
\[\frac{\partial \vec{p}}{\partial t} = \frac{\partial (\gamma mc\vec{\beta})}{\partial t} = q\left[ \vec{E} + \vec\beta\times\vec{B} \right]\]
## 5 Electrodynamics
### 5.1 Slowly Varying Fields
**Definition 5.1.1 ** The **electromotive force** $\varepsilon_{EMF}$ or **electromotive voltage** is the force per unit charge integrated along a loop moving at velocity $\vec{v}$.
\[\varepsilon_{EMF} = \oint\frac{F}{q}\cdot d\vec{\ell}=\oint\left[ \vec{E} + \vec{v}\times\vec{B} \right]\cdot d\vec{\ell}\]
**Definition 5.1.2 ** The **magnetic flux** $\Phi_B$ is the integral of the magnetic field $\vec{B}$ dotted with the normal vector for a surface $S$.
\[\Phi_B = \int_{S}\vec{B}\cdot d\vec{S}\]
**Law 5.1.3 ** **Faraday's law of induction** states that the electromotive force around a loop of wire $\varepsilon_{EMF}$ is equal to the negative time derivative of a slowly varying magnetic flux $\Phi$ through a surface $S$ bounded by the loop.
\[\varepsilon_{EMF} = -\frac{\partial \Phi_B}{\partial dt}\]
**Result 5.1.4 ** The **time derivative of the magnetic flux** can be rewritten as the following two integrals of the surface $S$ and boundary path $P$.
\[-\frac{\partial \Phi_B}{\partial dt} = - \int_S\frac{\partial \vec{B}}{\partial t}\cdot d\vec{S} - \oint_P(\vec{v}\times \vec{B})\cdot d\vec{P}\]
**Law 5.1.5 ** The **expanded Faraday's law of induction** states that transformer electromotive force is equal to the time derivative of a slowly varying transformer magnetic flux.
\[\oint\vec{E}\cdot d\vec{\ell} = - \int_S\frac{\partial \vec{B}}{\partial t}\cdot d\vec{S}\]
**Definition 5.1.6 ** The **displacement current density** $\vec{J}_D$ is the effective current density of a changing electric field.
\[\vec{J}_D = \varepsilon_0\frac{\partial \vec{E}}{\partial t}\]
**Result 5.1.7 ** The **magnetic field with displacement current** is the result of Stokes theorem to Maxwell's equations and displacement current density for slowly varying fields.
\[\oint\vec{B}\cdot d\vec{\ell} = \mu_0 \int_S \left(\vec{J} + \vec{J}_D\right)\cdot d\vec{S}\]
\[\oint\vec{B}\cdot d\vec{\ell} =\mu_0 \int_S \vec{J} \cdot d\vec{S} + \mu_0\varepsilon_0 \int_S \frac{\partial \vec{E}}{\partial t}\cdot d\vec{S}\]
### 5.2 Retarded Time
**Definition 5.2.1 ** The **retarded time** $t'$ is the time in the past that position $r'$ appears at when observed from position $r$ and time $t\newcommand\abs[1]{\left|#1\right|}$ due to speed of light $c$ delay.
\[t' = t - \frac{\abs{\vec{r}-\vec{r}'}}{c}\]
**Law 5.2.2 ** The **wave equations for electric potential $V$ and magnetic potential $\vec{A}$** describes how the potentials behave with time varying charge density $\rho$ and current density $\vec{J}$.
\[\nabla^2V - \mu_0\varepsilon_0\frac{\partial^2 V}{\partial t^2} = -\frac{\rho}{\varepsilon_0}\]
\[\nabla^2\vec{A}-\mu_0\varepsilon_0\frac{\partial^2 \vec{A}}{\partial t^2} = -\mu_0\vec{J}\]
\[\vec{\nabla}\cdot\vec{A} +\mu_0\varepsilon_0\frac{\partial V}{\partial t} = 0\]
**Result 5.2.3 ** A Time dependent **[Green's function](https://kaedon.net/l/^1mfe) for the [Laplace operator](https://kaedon.net/l/^59d9)** $G(\vec{r},\vec{r}',t,t')$ is the following function. $\newcommand\abs[1]{\left|#1\right|}$
\[G(\vec{r},\vec{r}',t,t') = \frac{\delta\left(t' - \left[ t - \frac{\abs{\vec{r}-\vec{r}'}}{c} \right]\right)}{\abs{\vec{r}-\vec{r}'}}\]
**Result 5.2.4 ** The **electric potential of a time dependent charge density** can be obtained by direct integration.$\newcommand\abs[1]{\left|#1\right|}$
\[V(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int{ \frac{\rho(\vec{r}',t')}{\abs{\vec{r}-\vec{r}'}} d^3r'}\]
\[V(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int{ \frac{\rho(\vec{r}',t - \frac{\abs{\vec{r}-\vec{r}'}}{c})}{\abs{\vec{r}-\vec{r}'}} d^3r'}\]
### 5.3 Jefimenko's Equations
**Definition 5.3.1 ** **Jefimenko's equations** are a series of integrals that can be used to evaluate the exact electric and magnetic field produced by a time varying charge density $\rho(\vec{r},t)$ and current density $\vec{J}(\vec{r},t)$.
**Result 5.3.2 ** **Jefimenko's equation for electric fields** describes the exact electric field $\vec{E}(\vec{r},t)$ produced by a time varying charge density $\rho(\vec{r},t)$ and current density $\vec{J}(\vec{r},t)$ where $t'$ is the [retarded time](https://kaedon.net/l/^ahc1#zfmr).
\[\vec{E}(\vec{r},t) = \vec{E}_{Coulomb}(\vec{r},t) + \vec{E}_{Charge}(\vec{r},t)+\vec{E}_{Current}(\vec{r},t)\newcommand\abs[1]{\left|#1\right|}\]
\[\vec{E}_{Coulomb}(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int \rho(\vec{r}',t')\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
\[\vec{E}_{Charge}(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int\left[ \frac{1}{c}\frac{\partial \rho(\vec{r}',t')}{\partial t'} \right] \frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^2}d^3r'\]
\[\vec{E}_{Current}(\vec{r},t)=-\frac{1}{4\pi\varepsilon_0}\int\left[\frac{1}{c^2}\frac{\partial \vec{J}(\vec{r}',t')}{\partial t'}\right]\frac{1}{\abs{\vec{r}-\vec{r}'}}d^3r'\]
**Result 5.3.3 ** **Alternate Jefimenko's equation for electric fields** describes the exact electric field $\vec{E}(\vec{r},t)$ produced by a time varying charge density $\rho(\vec{r},t)$ and current density $\vec{J}(\vec{r},t)$. When $\nabla\cdot\vec{J} = 0 $, $\vec{E}_{Currrent1} = 0$ where $t'$ is the [retarded time](https://kaedon.net/l/^ahc1#zfmr).
\[\vec{E}(\vec{r},t) = \vec{E}_{Coulomb}(\vec{r},t)+\vec{E}_{Current1}(\vec{r},t)+\vec{E}_{Current2}(\vec{r},t)\newcommand\abs[1]{\left|#1\right|}\]
\[\vec{E}_{Coulomb}(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int \rho(\vec{r}',t')\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
\[\vec{E}_{Current1}(\vec{r},t)=\frac{1}{4\pi\varepsilon_0c}\int\frac{\left[\vec{J}(\vec{r}',t')\cdot(\vec{r}-\vec{r}')\right](\vec{r}-\vec{r}')+\left[\vec{J}(\vec{r}',t')\times(\vec{r}-\vec{r}')\right]\times(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^4}d^3r'\]
\[\vec{E}_{Current2}(\vec{r},t)=\frac{1}{4\pi\varepsilon_0c^2}\int\frac{\left[\frac{\partial \vec{J}(\vec{r}',t')}{\partial t'}\times(\vec{r}-\vec{r}')\right]\times(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
**Result 5.3.4 ** **Jefimenko's equation for magnetic fields** describes the exact magnetic field $\vec{B}(\vec{r},t)$ produced by a time varying charge density $\rho(\vec{r},t)$ and current density $\vec{J}(\vec{r},t)$ where $t'$ is the [retarded time](https://kaedon.net/l/^ahc1#zfmr).
\[\vec{B}(\vec{r},t) = \vec{B}_{BiotSavart}(\vec{r},t) + \vec{B}_{Current}(\vec{r},t)\newcommand\abs[1]{\left|#1\right|}\]
\[\vec{B}_{BiotSavart}(\vec{r},t) = \frac{\mu_0}{4\pi}\int\vec{J}(\vec{r}',t')\times\left[\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}\right]d^3r'\]
\[\vec{B}_{Current}(\vec{r},t) = \frac{\mu_0}{4\pi}\int\left[ \frac{1}{c} \frac{\partial \vec{J}(\vec{r}',t')}{\partial t'}\right]\times\left[\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^2}\right]d^3r'\]
**Result 5.3.5 ** The **quasistatic expanded Jefimenko's equation** is an expansion of Jefimenko's equations that approximates the electric field $\vec{E}(\vec{r},t)$ and magnetic field $\vec{B}(\vec{r},t)$ produced by a time varying charge density $\rho(\vec{r},t)$ and current density $\vec{J}(\vec{r},t)$ where $t'$ is the [retarded time](https://kaedon.net/l/^ahc1#zfmr).$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{E}(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int\left(\rho(\vec{r}',t) - \frac{\abs{\vec{r}-\vec{r}'}^2}{2c^2}\frac{\partial^2\rho(\vec{r}',t)}{\partial t^2} + \cdots\right)\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
\[+\frac{\mu_0}{4\pi}\int\frac{\partial \vec{J}(\vec{r}',t)}{\partial t}\frac{1}{\abs{\vec{r}-\vec{r}'}}+\cdots d^3r'\]
\[\vec{B}(\vec{r},t) = \frac{\mu_0}{4\pi}\int\left[\vec{J}(\vec{r}',t)-\frac{\abs{\vec{r}-\vec{r}'}^2}{2c^2}\frac{\partial^2\vec{J}(\vec{r}',t)}{\partial t^2}\right]\times\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
### 5.4 Electromagnetic Energy and Momentum
**Definition 5.4.1 ** The **electromagnetic energy density** $u$ is the energy density of the electromagnetic fields at a particular point defined in terms of the electric field $\vec{E}$, the electric displacement field $\vec{D}$, the magnetic field $\vec{B}$ and the magnetic field strength $\vec{H}$.
\[u = \frac{\vec{E}\cdot \vec{D} + \vec{B}\cdot\vec{H}}{2}\]
**Result 5.4.2 ** In a **electromagnetic energy density in a vacuum** $u$ can be written in terms of the electric field $\vec{E}$ and magnetic field $\vec{B}$.
\[u = \frac{\varepsilon_0\vec{E}\cdot\vec{E} + \vec{B}\cdot\vec{B}/\mu_0}{2}\]
**Definition 5.4.3 ** The **Poynting vector** $\vec{S}$ is the energy flux (energy per unit area per unit time) of electromagnetic fields at a particular point defined in terms of the electric field $\vec{E}$ and magnetic field strength $\vec{H}$.
\[\vec{S} = \vec{E}\times\vec{H}\]
**Result 5.4.4 ** The **Poynting vector in a vacuum** $\vec{S}$ can be written in terms of the electric field $\vec{E}$ and magnetic field $\vec{B}$.
\[\vec{S} = \frac{\vec{E}\times\vec{B}}{\mu_0}\]
**Law 5.4.5 ** The **electromagnetic conservation of energy law** states that energy is conserved by electromagnetic fields.
\[\frac{\partial u}{\partial t} + \nabla\cdot\vec{S} = -\vec{J}\cdot\vec{E}\]
\[\vec{J}\cdot\vec{E} + \frac{\partial u}{\partial t} = -\nabla\cdot\vec{S}\]
**Definition 5.4.6 ** The **electromagnetic momentum density** $\vec{g}$ is the momentum density of the electromagnetic fields at a particular point defined in terms of the electric field $\vec{E}$ and magnetic field strength $\vec{H}$.
\[\vec{g} = \frac{\vec{E}\times\vec{H}}{c^2} = \frac{\vec{S}}{c^2}\]
**Definition 5.4.7 ** The **Maxwell stress tensor** or **momentum flux tensor** $T_{ij}$ is the 3 by 3 matrix describing the momentum flux (momentum per unit area per unit time) that is the change in each component of momentum in each direction defined by the the electric field $\vec{E}$ and magnetic field $\vec{B}$ in a vacuum.
\[T_{ij} = \varepsilon_0\left[ E_iE_j + c^2 B_iB_j - \frac{1}{2}\left(\vec{E}\cdot\vec{E} + c^2\vec{B}\cdot\vec{B}\right)\delta_{i,j}\right]\]
**Law 5.4.8 ** The **electromagnetic conservation of momentum law** states that momentum is conserved by electromagnetic fields.
\[\frac{d\vec{p}_{mech}}{dt} = q(\vec{E} + \vec{v}\times\vec{B})\]
\[\vec{p}_{field} = \varepsilon_0\int_V\vec{E}\times\vec{B} dV = \int_V \vec{g} dV\]
\[\left[ \frac{d\vec{p}_{mech}}{dt} + \frac{d \vec{p}_{field}}{dt}\right]\cdot \hat{k} = \oint_S\sum_jT_{k,j}n_j dS\]
where $k\in\{x,y,z\}$ and $\hat{n}$ is the vector pointing out of the surface $S$ that bounds the volume $V$.
**Definition 5.4.9 ** The **Maxwell stress 4-tensor** $\Omega^{\alpha,\beta}$ is the 4-tensor that can be used to describe the energy and momentum of electromagnetic fields in different reference frames.
\[\Omega = \begin{pmatrix} u & c\vec{g} \\ c\vec{g} & -T \end{pmatrix} =
\begin{pmatrix}
u & cg_x & cg_y & cg_z\\
cg_x & -T_{xx} & -T_{xy} & T_{xz}\\
cg_y & -T_{yx} & - T_{yy} & - T_{yz}\\
cg_z & -T_{zx} & -T_{zy} & -T_{zz}
\end{pmatrix}\]
**Result 5.4.10 ** The **Lorentz boost of a 4-tensor** can be computed by applying the [Lorentz boost matrix](https://kaedon.net/l/^ahc1#059k) $\Lambda(\vec\beta)$ to a 4-tensor $T$.
\[T' = \Lambda(\vec{\beta})T\Lambda^\top\]
### 5.5 Multipole Radiation
**Result 5.5.1 ** The **power radiated from a rotating multipole** $P_{radiated}$ can be written in terms of the oscillation frequency and the multipole expansion $\vec{p},\vec{m},Q_{jk},\cdots\newcommand\abs[1]{\left|#1\right|}$ of the charge distribution.
\[P_{radiated} = \frac{Z_0\omega^4}{12\pi c^4}\left[ \abs{\vec{p}}^2 + \abs{\frac{\vec{m}}{c}}^2 + \frac{\omega^2}{120 c^2}\sum_{jk}\abs{Q_{jk}}^2 + \cdots \right]\]
**Result 5.5.2 ** The **solid angle distribution of multipole radiation** describes the angular distribution of the power radiated by a rotating multipole.
\[\frac{\partial P}{\partial \Omega} \propto \omega^4 q^2 (r')^2\sin^2(\theta)\]
\[\frac{\partial P}{\partial \Omega} \propto \omega^4\left[ \frac{I}{c}(r') \right]^2(r')^2\sin^2(\theta)\]
\[\frac{\partial P}{\partial \Omega} \propto \omega^4\left[ \omega\frac{q}{c}(r') \right]^2(r')^2\sin^2(\theta)\cos^2(\theta)\]
**Definition 5.5.3 ** The **vector spherical harmonics** $\vec{X}_{\ell,m}(\theta,\phi)$ are generalizations of spherical harmonics for vectors fields.
\[\vec{X}_{\ell,m}(\theta,\phi) = \frac{-i(\vec{r}\times\nabla)Y_{\ell,m(\theta,\phi)}}{\sqrt{\ell(\ell + 1)}}\]
**Result 5.5.4 ** The **general electromagnetic multipole radiation** generated by electric multiple moments $a_M^{\ell,m}$ and magnetic multipole moments $a_E^{\ell,m}$ oscillating at frequency $\omega$ can be written in terms of [Vector Spherical Harmonics](https://kaedon.net/l/^ahc1#pa5a) $\vec{X}_{\ell,m}(\theta,\phi)$.
\[\vec{E} = \text{Real}\left( \sqrt{\frac{\mu_0}{\varepsilon_0}} \sum_{\ell,m}\left[ a_E^{\ell,m}\nabla\times\left( \frac{i}{k}f_\ell(kr)\vec{X}_{\ell,m} \right) + a_M^{\ell,m}g_\ell(kr) \vec{X}_{\ell,m} \right] e^{-i\omega t} \right)\]
\[\vec{B} = \text{Real}\left( \mu_0\sum_{\ell,m}\left[ -a_E^{\ell,m}\nabla\times\left( \frac{i}{k}g_\ell(kr)\vec{X}_{\ell,m} \right) + a_M^{\ell,m}f_\ell(kr) \vec{X}_{\ell,m} \right] e^{-i\omega t} \right)\]
\[f_\ell(kr) = A_\ell^{(1)}H_\ell^{(1)}(kr) + A_\ell^{(2)}H_\ell^{(2)}(kr)\]
\[g_\ell(kr) = B_\ell^{(1)}H_\ell^{(1)}(kr) + B_\ell^{(2)}H_\ell^{(2)}(kr)\]
\[k = \frac{\omega}{c}\]
where $A_\ell^{(1)}, A_{\ell}^{(2)}, B_\ell^{(1)}, B_\ell^{(2)}$ are coefficients determined by boundary conditions and $H_\ell^{(1)}, H_\ell^{(2)}$ are [Hankel functions](https://kaedon.net/l/^ahc1#emjk).
**Result 5.5.5 ** The **electric multipole moment $a_E^{\ell,m}$ due to an oscillating charge density** $\rho$ oscillating at angular frequency $\omega$ (wavenumber $k=\omega/c$) can be written as integrals of [spherical harmonics](https://kaedon.net/l/^ahc1#hae2) $Y_{\ell,m}^*$ and [Bessel functions](https://kaedon.net/l/^ahc1#et2j) $J_{\ell + 1/2}$. The multipole moment can be approximated when the wavelength is much greater that the size of the source.
\[a_E^{\ell,m} = \frac{k^2}{i\sqrt{\ell(\ell + 1)}} \int Y_{\ell,m}^*(\theta,\phi)\left[ c \rho(\vec{r}) \sqrt{\frac{\pi}{2kr}}\frac{\partial \left(r J_{\ell + 1/2}(kr)\right)}{\partial r}\right] d^3r\]
\[a_E^{\ell,m}\approx\frac{ck^{\ell+2}}{i(2\ell + 1)!!}\sqrt{\frac{\ell + 1}{\ell}}\int r^\ell Y_{\ell,m}^*(\theta,\phi)\rho(\vec{r})d^3r\]
**Result 5.5.6 ** The **multipole moment $a_E^{\ell,m},a_M^{\ell,m}$ due to an oscillating current density** $\vec{J}$ oscillating at angular frequency $\omega$ (wavenumber $k=\omega/c$) can be written as integrals of [spherical harmonics](https://kaedon.net/l/^ahc1#hae2) $Y_{\ell,m}^*$ and [Bessel functions](https://kaedon.net/l/^ahc1#et2j) $J_{\ell + 1/2}$. The multipole moment can be approximated when the wavelength is much greater that the size of the source.
\[a_E^{\ell,m} = \frac{k^2}{i\sqrt{\ell(\ell + 1)}}\int Y_{\ell,m}^*(\theta,\phi)\left[ ik\vec{r}\cdot\vec{J}(\vec{r})\sqrt{\frac{\pi}{2kr}}J_{\ell + 1/2}(kr) \right] d^3r\]
\[a_E^{\ell,m} \approx 0\]
\[a_M^{\ell,m} = \frac{k^2}{i\sqrt{\ell(\ell + 1)}}\int Y_{\ell,m}^*(\theta,\phi)\left[ \nabla \cdot \left( \vec{r}\times\vec{J}(\vec{r})\right) \sqrt{\frac{\pi}{2kr}}J_{\ell + 1/2}(kr)\right] d^3r\]
\[a_M^{\ell,m}\approx \frac{ik^{\ell+2}}{(2\ell + 1)!!}\sqrt{\frac{\ell}{\ell + 1}}\int (r)^\ell Y_{\ell,m}^*(\theta,\phi)\nabla\cdot\left( \vec{J}\times\vec{r} \right) d^3r\]
**Result 5.5.7 ** The **multipole moment $a_E^{\ell,m},a_M^{\ell,m}$ due to an oscillating magnetization** $\vec{M}$ oscillating at angular frequency $\omega$ (wavenumber $k=\omega/c$) can be written as integrals of [spherical harmonics](https://kaedon.net/l/^ahc1#hae2) $Y_{\ell,m}^*$ and [Bessel functions](https://kaedon.net/l/^ahc1#et2j) $J_{\ell + 1/2}$. The multipole moment can be approximated when the wavelength is much greater that the size of the source.
\[a_E^{\ell,m} = \frac{k^2}{i\sqrt{\ell(\ell + 1)}} \int Y_{\ell,m}^*(\theta,\phi)\left[ -ik\nabla\cdot\left( \vec{r}\times\vec{M}(\vec{r}) \right) \sqrt{\frac{\pi}{2kr}}J_{\ell+1/2}(kr) \right] d^3r\]
\[a_E^{\ell,m} \approx -\frac{k^{\ell + 2}}{(2\ell + 1)!!}\sqrt{\frac{1}{\ell(\ell + 1)}}\int(r)^\ell Y_{\ell,m}^*(\theta,\phi)\left[ \nabla\cdot(\vec{r}\times\vec{M}(\vec{r})) \right] d^3r\]
\[a_M^{\ell,m} = \frac{k^2}{i\sqrt{\ell(\ell+1)}}\int Y_{\ell,m}^*(\theta,\phi)\left[ -k^2\left(\vec{r}\cdot\vec{M}(\vec{r})\right)\sqrt{\frac{\pi}{2kr}}J_{\ell + 1/2}(kr) \right]d^3r\]
\[a_M^{\ell,m}\approx -\frac{ik^{\ell+2}}{(2\ell+1)!!}\sqrt{\frac{\ell + 1}{\ell}}\int (r)^\ell Y_{\ell,m}^*(\theta,\phi)\left( \nabla\cdot\vec{M}(\vec{r}) \right)d^3r\]
### 5.6 Moving Charges
**Result 5.6.1 ** The **electromagnetic fields from an accelerating point charge** at position $\vec{r}_{charge}$ observed at position $\vec{r}_{obs}$ can be written as the following two terms. The first term is the "velocity field" which dominates in the quasi-static regime and the second term is the "acceleration field" which dominates in the radiation regime.
\[\vec{E} = \frac{q}{4\pi\varepsilon_0}\left[\frac{\beta}{\gamma^2 R^2}\cdot\frac{\hat{R}/\beta - \hat{\beta}}{\left(1-\vec{\beta}\cdot\hat{R}\right)^3}\right]_{ret} + \frac{q}{4\pi\varepsilon_0}\left[\frac{\beta\dot{\beta}}{cR}\cdot\frac{\hat{R}\times\left( \left(\hat{R}/\beta - \hat{\beta}\right)\times\dot{\hat{\beta}} \right)}{\left(1-\vec{\beta}\cdot\hat{R}\right)^3}\right]_{ret}\]
\[c\vec{B} = \left[\hat{R}\times\vec{E}\right]_{ret}\]
\[\vec{R} = \vec{r}_{obs}-\vec{r}_{charge}\]
**Definition 5.6.2 ** The **Larmor power** $P_{Larmor}$ is the power radiated by an accelerating particle with acceleration $\dot{\beta}$ in the non-relativistic limit.
\[P_{Larmor} = \frac{q^2 \dot\beta^2}{6\pi\varepsilon_0 c}\]
**Result 5.6.3 ** The **relativistic Larmor formula** describes the power radiated $P_{rad}\newcommand\abs[1]{\left|#1\right|}$ by a relativistic accelerating particle.
\[P_{rad} = \gamma^6\left[1-\abs{\hat{\beta}\times\hat{\dot{\beta}}}^2\beta^2\right]P_{Larmor} = \gamma^6\left[1-\abs{\hat{\beta}\times\hat{\dot{\beta}}}^2\beta^2\right] \frac{q^2 \dot\beta^2}{6\pi\varepsilon_0 c}\]
\[\frac{dP_{rad}}{d\Omega} = \frac{q^2}{16\pi^2\varepsilon_0c}\frac{\abs{\hat{R}\times\left(\left(\hat{R}-\vec{\beta}\right)\times\dot{\vec{\beta}}\right)}^2}{\left(1-\hat{R}\cdot\vec{\beta}\right)^5}\]
\[\vec{R} = \vec{r}_{obs}-\vec{r}_{charge}\]
## 6 Appendix
### 6.1 References
[^32ca]
[^32ca]: Richard S. Davis; Determining the value of the fine-structure constant from a current balance: Getting acquainted with some upcoming changes to the SI. Am. J. Phys. 1 May 2017; 85 (5): 364–368. https://doi.org/10.1119/1.4976701
**File 2.8.2 ** Relaxation.PNG
### 2.9 Finite Element Method
**Definition 2.9.1 ** The **finite element method** is a computational method for calculating an approximation of the solution to a differential equation with a finite mesh to represent the geometry of the system.
### 2.10 Green's Function Theory
**Definition 2.10.1 ** A **linear differential operator** is a functional operator involving differentiation that is [linear](https://kaedon.net/l/^n96p).
**Definition 2.10.2 ** The **Green's function** denoted $G$ for a linear operator $\mathcal{L}$ is the solution to the following equation where $\delta$ is the [Dirac delta](https://kaedon.net/l/^wna1).
\[\mathcal{L}G(\vec{r},\vec{r}')=-4\pi\delta(\vec{r}-\vec{r}')\]
**Corollary 2.10.3 ** Let $G(\vec{r},\vec{r}')$ be a [Green's function](https://kaedon.net/l/^1mfe) for a [linear differential operator](https://kaedon.net/l/^3r0m) $\mathcal{L}$ and $F(\vec{r},\vec{r}')$ be any function such that $\mathcal{L}F=0$, then the function $G'(\vec{r},\vec{r}')$ defined below is also a Green's function for $\mathcal{L}$.
\[G'(\vec{r},\vec{r}') = G(\vec{r},\vec{r}') + F(\vec{r},\vec{r}')\]
**Definition 2.10.4 ** The **differential form for Green's function theory** is the following differential form solving for $u(\vec{r})$ where $\mathcal{L}$ is a linear differential operator and $f(\vec{r})$ is an arbitrary distribution.
\[\mathcal{L}u(\vec{r})=f(\vec{r})\]
**Theorem 2.10.5 ** The solution to a differential equation of the [form](https://kaedon.net/l/^fh5f) $\mathcal{L}u(\vec{r})=f(\vec{r})$ is the integral of the [Green's function](https://kaedon.net/l/^1mfe) $G$ of the [linear differential operator](https://kaedon.net/l/3r0m) $\mathcal{L}$ and the distribution $f(\vec{r})$.
\[u(\vec{r}) = -\frac{1}{4\pi}\int{ f(\vec{r}')G(\vec{r},\vec{r}') d^3r'}\]
**Result 2.10.6 ** A **[Green's function](https://kaedon.net/l/^1mfe) for the [Laplace operator](https://kaedon.net/l/^59d9)** $G(\vec{r},\vec{r}')$ is the following function. $\newcommand\abs[1]{\left|#1\right|}$
\[G(\vec{r},\vec{r}') = \frac{1}{\abs{\vec{r}-\vec{r}'}}\]
**Result 2.10.7 ** The **electric potential of a charge density** can be obtained by direct integration.$\newcommand\abs[1]{\left|#1\right|}$
\[V(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int{ \frac{\rho(\vec{r}')}{\abs{\vec{r}-\vec{r}'}} d^3r'}\]
**Theorem 2.10.8 ** The solution to a differential equation of the form $\mathcal{L}u(\vec{r}) = f(\vec{r})$ in the volume $V$ with boundary conditions on surface $S$ is the sum of the following integrals of a [Green's function](https://kaedon.net/l/1mfe) $G$ of the linear differential operator $\mathcal{L}$ and the arbitrary function $f(\vec{r})$, where $\hat{n}$ is the normal vector of the surface $S$ pointing outward from the volume $V$.
\[u(\vec{r}) = -\frac{1}{4\pi}\int_{V}{ f(\vec{r}')G(\vec{r},\vec{r}') d^3r'} + \frac{1}{4\pi}\oint_S\left[\frac{\partial u(\vec{r}')}{\partial n'}\right]G(\vec{r},\vec{r}')d^2r' - \frac{1}{4\pi}\oint_S\left[u(\vec{r}')\right]\frac{\partial G(\vec{r},\vec{r}')}{\partial n'}d^2r'\]
**Result 2.10.9 ** The **electric potential of the charge distribution with boundary conditions** can be obtain by direct integration with an appropriate choice of [Green's function](https://kaedon.net/l/1mfe) $G$ for the Laplace operator $\nabla^2$. Let $A$ be the volume of interest, $S$ be the boundary surface of $A$ and $\rho(\vec{r})$ be the charge density inside the volume $A$. The electric potential is determined by the following integrals of Green's functions.
\[V(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int_{A}{ \rho(\vec{r}')G(\vec{r},\vec{r}') d^3r'} + \frac{1}{4\pi}\oint_S\left[\frac{\partial V(\vec{r}')}{\partial n'}\right]G(\vec{r},\vec{r}')d^2r' - \frac{1}{4\pi}\oint_S\left[V(\vec{r}')\right]\frac{\partial G(\vec{r},\vec{r}')}{\partial n'}d^2r'\]
**Definition 2.10.10 ** The **Dirichlet condition** is the boundary condition where the potential $V(\vec{r})$ on the bounding surface is known.
**Definition 2.10.11 ** The **Neumann condition** is the boundary condition where the normal derivative of the potential $\frac{\partial V(\vec{r})}{\partial n}$ on the bounding surface is known.
**Result 2.10.12 ** The **electric potential $V(\vec{r})$ caused by a sphere with known potential** can be calculated with integrals of the following [Green's Function](https://kaedon.net/l/^ahc1#1mfe) $G(\vec{r},\vec{r}')$ for the volume $A$ inside or outside a sphere of radius $R$ centered at the origin with bounding surface $S$, where $\hat{n}$ is the normal vector of the surface $S$ pointing outward from the volume $V$.
\[G(\vec{r},\vec{r}') = \frac{1}{\abs{\vec{r}-\vec{r}'}} - \frac{\frac{R}{r'}}{\abs{\vec{r}-\frac{R^2}{r'^2}\vec{r}'}}\]
\[\left.\frac{\partial G(\vec{r},\vec{r}')}{\partial n'}\right|_{r'=R} = \frac{-\abs{r^2 - R^2}}{R\left(r^2+R^2-2Rr\left[\cos\theta\cos\theta'+\sin\theta\sin\theta'\cos(\phi-\phi')\right]\right)^{3/2}}\]
\[V(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int_{A}{ \rho(\vec{r}')G(\vec{r},\vec{r}') d^3r'} - \frac{1}{4\pi}\oint_S\left[V(\vec{r}')\right]\frac{\partial G(\vec{r},\vec{r}')}{\partial n'}d^2r'\]
## 3 Magnetostatics
### 3.1 Magnetic Field
**Definition 3.1.1 ** The **magnetic field** or **magnetic flux density** denoted $\vec{B}$ is the vector field that describes the force per length of current in a region of space. This is the actual magnetic field at a point in space.
**Definition 3.1.2 ** The **magnetic field strength** denoted $\vec{H}$ is the vector that described the external contribution to the magnetic field in a material not intrinsic to the material's magnetization $\vec{M}$, where $\mu_0$ is the vacuum permeability.
\[\vec{H} = \frac{\vec{B}}{\mu_0} - \vec{M}\]
**Definition 3.1.3 ** A **surface current density** denoted $\vec{K}(\vec{r})$ is a vector field describing the density of current flowing on a surface.
**Result 3.1.4 ** The current $I$ crossing a line $L$ on a surface $S$ with surface current density $\vec{K}(\vec{r})$ is given by the following path integral relative to a unit vector $\hat{n}$ pointing from the origin to each point on the line.
\[I = \int_L (\vec{K}\times\hat{n})\cdot d\vec{L}\]
**Definition 3.1.5 ** A **volume current density** denoted $\vec{J}(\vec{r})$ is a vector field describing the density of current flowing at a particular point in space.
**Result 3.1.6 ** The current $I$ passing through a surface $S$ in a space with volume current density $\vec{J}(\vec{r})$ is given by the following surface integral.
\[I = \int_S \vec{J}\times d\vec{S}\]
**Law 3.1.7 ** The **Biot-Savart law** states that the magnetic field $\vec{B}$ produced by a current carrying wire, a surface current density $\vec{K}(\vec{r}')$ or a volume current density $\vec{J}(\vec{r})$ in a vacuum is determined by the following integrals.$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{B} = \frac{\mu_0I}{4\pi}\int_L\frac{d\vec{r}'\times\left(\vec{r}-\vec{r}'\right)}{\abs{\vec{r}-\vec{r}'}^3}\]
\[\vec{B} = \frac{\mu_0}{4\pi}\int_S\frac{\vec{K}(\vec{r}')\times(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^2\vec{r}'\]
\[\vec{B} = \frac{\mu_0}{4\pi}\int_V\frac{\vec{J}(\vec{r}')\times(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3\vec{r}'\]
**Law 3.1.8 ** **Ampere's circuit law** states that the loop integral of the magnetic field along a loop $C$ is equal to the surface integral of the current flux out of a surface $S$ bounded by $C$. This is a consequence of [Stoke's theorem](https://kaedon.net/l/7ahh) and [Maxwell's equations](https://kaedon.net/l/3a2h).
\[\oint_C\vec{B}\cdot d\vec{\ell} = \mu_0\int_S\vec{J}\cdot d\vec{S} = \mu_0I_{\text{enclosed}}\]
**Result 3.1.9 ** The **force $\vec{F}$ on a current carrying wire** with current $I$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following path integral:
\[\vec{F} = I\int{d\vec{\ell}\times \vec{B}(\vec{r}')}\]
**Result 3.1.10 ** The **torque $\vec{N}$ on a current density $\vec{J}(\vec{r})$** around a pivot point $\vec{r}_p$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following integral:
\[\vec{N}(\vec{r}_p) = \int \left[\vec{r}' - \vec{r}_p'\right]\times \left[\vec{J}(\vec{r}')\times\vec{B}(\vec{r}')\right]d^3r'\]
### 3.2 Magnetic Forces
**Law 3.2.1 ** The **Lorentz force law** states that the force $\vec{F}$ on a charged particle with charge $q$ moving at velocity $\vec{v}$ through magnetic field $\vec{B}$ is determined by the following cross product.
\[\vec{F} = q\vec{v}\times\vec{B}\]
**Result 3.2.2 ** The **force $\vec{F}$ on a current density $\vec{J}(\vec{r})$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following integral:
\[\vec{F} = \int{\vec{J}(\vec{r}')\times\vec{B}(\vec{r}')d^3r'}\]
**Result 3.2.3 ** The **force $\vec{F}$ on a current carrying wire** with current $I$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following path integral:
\[\vec{F} = I\int{d\vec{\ell}\times \vec{B}(\vec{r}')}\]
**Result 3.2.4 ** The **torque $\vec{N}$ on a current density $\vec{J}(\vec{r})$** around a pivot point $\vec{r}_p$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following integral:
\[\vec{N}(\vec{r}_p) = \int \left[\vec{r}' - \vec{r}_p'\right]\times \left[\vec{J}(\vec{r}')\times\vec{B}(\vec{r}')\right]d^3r'\]
**Result 3.2.5 ** The **torque $\vec{N}$ on a current carrying wire** with current $I$ around a pivot point $\vec{r}_p$ in a magnetic field $\vec{B}(\vec{r})$ is given by the following path integral:
\[\vec{N}(\vec{r}_p) = I \int \left[\vec{r}' - \vec{r}_p'\right]\times \left[d\vec{\ell}'\times\vec{B}(\vec{r}')\right]\]
### 3.3 Magnetic Potential
**Definition 3.3.1 ** The **magnetic potential** denoted $\vec{A}(\vec{r},t)$ is a vector potential such that the curl of the potential is the magnetic field.
\[\vec{B} = \nabla \times \vec{A}\]
**Definition 3.3.2 ** A **gauge** is a any choice of configuration of the unobservable fields that does not affect the observable fields.
**Definition 3.3.3 ** A **gauge transformation** is any transformation of the unobservable fields that does not affect the observable fields.
**Result 3.3.4 ** Any **arbitrary gauge transformation** acting on magnetic potential $\vec{A}(\vec{r},t)$ and electric potential $V(\vec{r},t)$ takes the following form for some scalar field $\Psi(\vec{r},t)$.
\[\vec{A}\to \vec{A} + \nabla\Psi\]
\[V \to V - \frac{\partial \Psi}{\partial t}\]
**Definition 3.3.5 ** The **Coulomb gauge** is the convention that $\nabla\cdot\vec{A} = 0$.
**Result 3.3.6 ** The **magnetic potential in the Coulomb gauge** can be directly integrated from the volume current density $\vec{J}$ or the magnetic field $\vec{B}$ with one of the following integrals.$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{A}(\vec{r}) = \frac{\mu_0}{4\pi}\int\frac{\vec{J}(\vec{r}')}{\abs{\vec{r}-\vec{r}'}}d^3r'\]
\[\vec{A}(\vec{r}) = \frac{1}{4\pi}\int\frac{\vec{B}(\vec{r}')\times(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
### 3.4 Magnetic Dipole Moment
**Definition 3.4.1 ** The **magnetic dipole moment** denoted $\vec{m}$ of a current density $\vec{J}(\vec{r})$ is defined with the following integral.
\[\vec{m} = \frac{1}{2}\int\vec{r}'\times\vec{J}(\vec{r}')d^3\vec{r}'\]
**Result 3.4.2 ** The **magnetic potential $\vec{A}$ of a magnetic dipole moment** $\vec{m}$ is given by the following formula.
\[\vec{A} = \frac{\mu_0}{4\pi} \frac{\vec{m}\times\vec{r}}{r^3}\]
**Result 3.4.3 ** The **magnetic field $\vec{B}$ of a magnetic dipole moment** $\vec{m}$ is given by the following formula where $\newcommand\abs[1]{\left|#1\right|}\hat{n} = \frac{\vec{r}-\vec{r}_m}{\abs{\vec{r}-\vec{r}_m}}$ is the unit vector pointing from the position of the magnetic dipole moment $\vec{r}_m$ and the observation point $\vec{r}$.
\[\vec{B}(\vec{r}) = \frac{\mu_0}{4\pi}\left[\frac{3\hat{n}\left(\hat{n}\cdot\vec{m}\right) - \vec{m}}{\abs{\vec{r}-\vec{r}_m}^3} + \frac{8\pi}{3}\vec{m}\delta^3(\vec{r}-\vec{r}_m)\right]\]
**Result 3.4.4 ** The **force $F$ on a magnetic dipole moment** $\vec{m}$ in a magnetic field $\vec{B}$ is given by the following dot product gradient.
\[\vec{F} = \nabla\left( \vec{m}\cdot\vec{B} \right)\]
**Result 3.4.5 ** The **torque $\vec{\tau}$ on a magnetic dipole moment** $\vec{m}$ in a magnetic field $\vec{B}$ is given by the following cross product.
\[\vec{\tau} = \vec{m}\times\vec{B}\]
### 3.5 Magnetic Quadrupole Field
**Definition 3.5.1 ** The **magnetic quadrupole field** is the magnetic field produced by four infinitely lone wire run parallel to the z-axis with currents $-I\hat{z}$ at $(0,\pm R,0)$ and $+I\hat{z}$ at $(\pm R,0,0)$.
\[\vec{B} = -\frac{2\mu_0 I}{\pi R} \left[\frac{y\hat{x}+x\hat{y}}{R}\right]\]
## 4 Special Relativity
### 4.1 Lorentz Transformations
**Definition 4.1.1 ** An **inertial reference frame** is a coordinate system that moves with a constant rectilinear velocity.
**Definition 4.1.2 ** The **simultaneity beta** denoted $\vec{\beta}$ is the vector $\vec{\beta} = \frac{\vec{v}}{c}$ where $v$ is the velocity of a reference frame and $c$ is the speed of light.
**Definition 4.1.3 ** The **simultaneity gamma** denoted $\gamma$ is the scalar $\gamma = \left(1-\beta^2\right)^{-1/2}$, where $\newcommand\abs[1]{\left|#1\right|}\beta=\abs{\vec{\beta}}$ is [simultaneity beta](https://kaedon.net/l/^ahc1#awac).
**Definition 4.1.4 ** A **Lorentz transformation** is a transformation $\Lambda:\mathbb{R}^{1,3}\to\mathbb{R}^{1,3}$ the preserves the scalar $(A_0-B_0)^2-(A_1-B_1)^2-(A_2-B_2)^2-(A_3-B_3)^2$ for all $A,B\in\mathbb{R}^{1,3}$.
**Definition 4.1.5 ** The **Poincaré group** or the **inhomogeneous Lorentz group** is the group of all [Lorentz transformations](https://kaedon.net/l/^ahc1#7823) such as translations, rotations and boosts.
**Definition 4.1.6 ** A **homogeneous Lorentz transformation** is a transformation $\Lambda:\mathbb{R}^{1,3}\to\mathbb{R}^{1,3}$ that preserves the scalar $A_0^2-A_1^2-A_2^2-A_3^2$ for all $A\in\mathbb{R}^{1,3}$.
**Definition 4.1.7 ** The **homogeneous Lorentz group** or sometimes simply the **Lorentz group** is the group of all [homogeneous Lorentz transformations](https://kaedon.net/l/^ahc1#59kr). This only includes linear transformations such as rotations and boosts, but not non-linear transformations such as translations.
**Proposition 4.1.8 ** [Homogeneous Lorentz transformations](https://kaedon.net/l/^ahc1#59kr) are [Lorentz transformations](https://kaedon.net/l/^ahc1#7823).
**Definition 4.1.9 ** The **Lortenz boost** $A\mapsto A'$ is a [homogeneous Lorentz transformation](https://kaedon.net/l/^ahc1#59kr) that transforms any [four vector](https://kaedon.net/l/^ahc1#m43n) $A\in\mathbb{R}^{1,3}$ to a four vector in a reference frame moving with relative velocity $\vec{v}$ and [simultaneity beta](https://kaedon.net/l/^ahc1#awac) $\vec\beta = \frac{\vec{v}}{c}$.
\[A_0' = \gamma(A_0 - \vec{\beta}\cdot\vec{A})\]
\[\vec{A}' = \vec{A}+\frac{(\gamma - 1)}{\beta^2}(\vec{\beta}\cdot\vec{A})\vec{\beta}-\gamma\vec{\beta}A_0\]
**Result 4.1.10 ** The [Lorentz boost](https://kaedon.net/l/^ahc1#5zte) $A\mapsto A'$ into a frame with relative velocity $\vec{v}$ and [simultaneity beta](https://kaedon.net/l/^ahc1#awac) $\vec\beta = \frac{\vec{v}}{c}$ can be written in terms of the component $A_\parallel$ of $A$ parallel to $\vec{\beta}$ and the component $A_\perp$ of $A$ perpendicular to $\vec{\beta}$ for $\gamma = \left(1-\beta^2\right)^{-1/2}$.
\[A'_0 = \gamma(A_0 - \vec{\beta}\cdot\vec{A})\]
\[A'_\parallel = \gamma(A_\parallel - \beta A_0)\]
\[\vec{A}'_{\perp} = \vec{A}'_\perp\]
**Result 4.1.11 ** The following **Lorentz boost matrix** $\Lambda(\vec{\beta})$ can be used to apply a [Lorentz boost](https://kaedon.net/l/^ahc1#5zte) $A\mapsto A'=\Lambda(\vec{\beta}) A$ to a four vector $A\in\mathbb{R}^{1,3}$ into a reference frame with relative velocity $\vec{v}$ and [simultaneity beta](https://kaedon.net/l/^ahc1#awac) $\vec\beta = \frac{\vec{v}}{c}$.
\[\Lambda(\vec{\beta}) = \begin{pmatrix} \gamma & -\gamma\beta_x & -\gamma\beta_y & -\gamma\beta_z \\
-\gamma\beta_x & 1+\frac{(\gamma-1)\beta_x^2}{\beta^2} & \frac{(\gamma-1\beta_x\beta_y)}{\beta^2} & \frac{(\gamma-1\beta_x\beta_z)}{\beta^2}\\
-\gamma\beta_y & \frac{(\gamma-1\beta_x\beta_y)}{\beta^2} & 1+\frac{(\gamma-1)\beta_y^2}{\beta^2} & \frac{(\gamma-1\beta_y\beta_z)}{\beta^2}\\
-\gamma\beta_z & \frac{(\gamma-1\beta_x\beta_z)}{\beta^2} & \frac{(\gamma-1\beta_y\beta_z)}{\beta^2} & 1+\frac{(\gamma-1)\beta_z^2}{\beta^2} \end{pmatrix}\]
### 4.2 Four Vectors
**Definition 4.2.1 ** A **four vector** is a vector $A=(A_0,\vec{A})\in\mathbb{R}^{1,3}$ of a time-like scalar component $A_0$ and a space-like vector component $\vec{A}=(A_1,A_2,A_3)$ where the quantity $A_0^2 -A_1^2 -A_2^2 -A_3^2$ is invariant for all reference frames and [homogeneous Lorentz transformations](https://kaedon.net/l/^ahc1#59kr).
**Definition 4.2.2 ** The **flat negative trace metric tensor** is the metric tensor that describes flat space for special relativity with the negative trace convention.
\[\eta = \begin{pmatrix}1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1\end{pmatrix}\]
**Definition 4.2.3 ** The **four vector dot product** for two four vectors $A,B\in\mathbb{R}^{1,3}$ is defined in terms of a metric tensor $\eta$.
\[A\cdot B = A^\top\eta B\]
**Definition 4.2.4 ** The **four vector norm** $\newcommand\abs[1]{\left|#1\right|}\abs{A}$ of a four vector $A\in\mathbb{R}^{1,3}$ is defined $\abs{A}=\sqrt{A\cdot A}$.
**Result 4.2.5 ** The dot product of any two four vectors is invariant under [Lorentz transformation](https://kaedon.net/l/^ahc1#59kr).
**Definition 4.2.6 ** The **4-position** is the four vector $(ct,\vec{r})$ with corresponding invariant **spacetime interval** $s^2=(ct)^2 - \abs{\vec{r}}^2$ where $c$ is the speed of light, $t$ is time and $\vec{r}$ is the position of a space-time coordinate.
**Definition 4.2.7 ** The **4-velocity** is the four vector $(\gamma_vc,\gamma_v\vec{v})$ with corresponding invariant $(\gamma_vc)^2 - \gamma_v^2\abs{\vec{v}}^2$, where $\gamma_v=\left(1-v^2/c^2\right)^{-1/2}$, $c$ is the speed of light and $\vec{v}$ is the velocity.
**Result 4.2.8 ** The **velocity addition law** describes how to combine the velocities of two objects in a way that is consistent with relativity.
**Definition 4.2.9 ** The **4-momentum** is the four vector $(E/c,\vec{p})$ with corresponding invariant $(E/c)^2 - \abs{\vec{p}}^2 = m^2c^2$ where $c$ is the speed of light, $m$ is the rest mass, $E$ is the energy and $\vec{p}$ is the momentum.
**Definition 4.2.10 ** The **4-current density** is the four vector $\left(c\rho,\vec{J}\right)$ with corresponding invariant $(c\rho)^2 - \abs{\vec{J}}^2$ where $c$ is the speed of light, $\rho$ is the charge density and $\vec{J}$ is the current density.
**Definition 4.2.11 ** The **4-wave vector** is the four vector $(\omega/c,\vec{k})$ with corresponding invariant $(\omega/c)^2 - \abs{\vec{k}}^2 = (mc/\hbar)^2$ where $c$ is the speed of light, $\omega$ is the frequency in radians per second, $\vec{k}$ is the wave vector and $m$ is the rest mass.
**Result 4.2.12 ** The phase of a wave $\phi = \omega t - \vec{k}\cdot\vec{r}$ is invariant under [Lorentz transformation](https://kaedon.net/l/^ahc1#59kr).
\[(ct,\vec{r})\cdot(\omega/c,\vec{k}) = \omega-\vec{k}\cdot\vec{r} = \phi\]
**Table 4.2.13 ** Four vectors and their corresponding invariants.$\newcommand\abs[1]{\left|#1\right|}$
| Four Vector | | Invarient | |
|:----------------|:---------|:-----------|:----------|
| 4-Position | $(ct,\vec{r})$ | Spacetime interval | $(ct)^2 - \abs{\vec{r}}^2 = s^2$ |
| 4-Velocity| $(\gamma_vc,\gamma_v\vec{v})$ | (no name) | $(\gamma_vc)^2 - \gamma_v^2\abs{\vec{v}}^2$ |
| 4-Momentum | $(E/c,\vec{p})$ | Rest mass squared | $(E/c)^2 - \abs{\vec{p}}^2 = m^2c^2$ |
| 4-Current Density | $\left(c\rho,\vec{J}\right)$ | (no name) | $(c\rho)^2 - \abs{\vec{J}}^2$ |
| 4-Wave Vector | $(\omega/c,\vec{k})$ | Rest mass over hbar squared | $(\omega/c)^2 - \abs{\vec{k}}^2 = (mc/\hbar)^2$ |
### 4.3 Einstein Notation
**Definition 4.3.1 ** **Einstein notation** or **Einstein summation notation** is a notational convention that used subscripts and superscripts to simplify summation notation over the implied range of that index. Paired indexes are summed over and unpaired indexes represent the components of the vector or tensor.
\[c_ix^i = \sum_{i=0}^3 c_ix^i = c_0x^0 + c_1x^1 + c_2x^2 + c_3x^3\]
**Definition 4.3.2 ** A **contravarient vector** is a four vector written in Einstein notation with the index in the superscript.
\[A^\mu = (A_0,\vec{A})\]
**Definition 4.3.3 ** A **covarient vector** is a four vector written in Einstein notation with the index in the subscript.
\[A_\mu = \eta_{\mu\nu}A^\nu = \sum_{\nu=0}^3\eta_{\mu\nu}A^\nu = (A_0,-\vec{A})\]
**Definition 4.3.4 ** The **scalar product** of two four vectors $a,b\in\mathbb{R}^{1,3}$ is simply the [four vector dot product](https://kaedon.net/l/^ahc1#pma4).
\[a\cdot b = a_\mu b^\mu = \eta_{\mu\nu}a^\nu b^\mu = \sum_{\mu =0}^3\sum_{\nu=0}^3\eta_{\mu\nu}a^\nu b^\mu = a_0b_0 - \vec{a}\cdot\vec{b}\]
### 4.4 Field Strength Tensor
**Definition 4.4.1 ** The **field strength tensor** $F$ is a 4-tensor that contains both the [electric field](https://kaedon.net/l/^ahc1#zf8f) and the [magnetic field](https://kaedon.net/l/^ahc1#h3d5) at a particular point in spacetime.
\[F = \begin{pmatrix} 0 & -E_x & -E_y & -E_z\\ +E_x & 0 & -B_z & +B_y \\ +E_y & +B_z & 0 & -B_x \\ +E_z & -B_y & +B_x & 0\end{pmatrix}\]
**Result 4.4.2 ** The **Lorentz boost of a 4-tensor** can be computed by applying the [Lorentz boost matrix](https://kaedon.net/l/^ahc1#059k) $\Lambda(\vec\beta)$ to a 4-tensor $T$.
\[T' = \Lambda(\vec{\beta})T\Lambda^\top\]
**Result 4.4.3 ** The **Lorentz boost of electric and magnetic fields** into a frame with relative velocity $\vec{v}$ and [simultaneity beta](https://kaedon.net/l/^ahc1#awac) $\vec\beta = \frac{\vec{v}}{c}$ can be calculated with the following formulas.
\[\vec{E}' = \gamma\left(\vec{E} + \vec\beta\times\vec{B}\right) - \frac{\gamma - 1}{\beta^2}\left(\vec\beta \cdot\vec{E}\right)\vec\beta\]
\[\vec{B}'=\gamma\left(\vec{B}-\vec\beta\times\vec{E}\right)-\frac{\gamma-1}{\beta^2}\left(\vec\beta\cdot\vec{B}\right)\vec\beta\]
**Result 4.4.4 ** The **Lorentz boost of electric and magnetic fields** into a frame with relative velocity $\vec{v}$ and [simultaneity beta](https://kaedon.net/l/^ahc1#awac) $\vec\beta = \frac{\vec{v}}{c}$ can be written in terms of the components $E_\parallel,B_\parallel$ of $E,B$ parallel to $\vec{\beta}$ and the components $E_\perp,B_\perp$ of $E,B$ perpendicular to $\vec{\beta}$.
\[\vec{E}'_\parallel = \vec{E}_\parallel\]
\[\vec{E}'_\perp = \gamma\left(\vec{E}_\perp + \vec\beta\times\vec{B}_\perp\right)\]
\[\vec{B}'_\parallel = \vec{B}_\parallel\]
\[\vec{B}'_\perp = \gamma\left(\vec{B}_\perp - \vec\beta\times\vec{E}_\perp\right)\]
**Result 4.4.5 ** The **relativistic motion in static electromagnetic fields** for a charged particle with rest mass $m$ and momentum $\vec{p}$ in electric and magnetic fields $\vec{E}$ and $\vec{B}$ the motion of this particles can be described by the following differential equation.
\[\frac{\partial \vec{p}}{\partial t} = \frac{\partial (\gamma mc\vec{\beta})}{\partial t} = q\left[ \vec{E} + \vec\beta\times\vec{B} \right]\]
## 5 Electrodynamics
### 5.1 Slowly Varying Fields
**Definition 5.1.1 ** The **electromotive force** $\varepsilon_{EMF}$ or **electromotive voltage** is the force per unit charge integrated along a loop moving at velocity $\vec{v}$.
\[\varepsilon_{EMF} = \oint\frac{F}{q}\cdot d\vec{\ell}=\oint\left[ \vec{E} + \vec{v}\times\vec{B} \right]\cdot d\vec{\ell}\]
**Definition 5.1.2 ** The **magnetic flux** $\Phi_B$ is the integral of the magnetic field $\vec{B}$ dotted with the normal vector for a surface $S$.
\[\Phi_B = \int_{S}\vec{B}\cdot d\vec{S}\]
**Law 5.1.3 ** **Faraday's law of induction** states that the electromotive force around a loop of wire $\varepsilon_{EMF}$ is equal to the negative time derivative of a slowly varying magnetic flux $\Phi$ through a surface $S$ bounded by the loop.
\[\varepsilon_{EMF} = -\frac{\partial \Phi_B}{\partial dt}\]
**Result 5.1.4 ** The **time derivative of the magnetic flux** can be rewritten as the following two integrals of the surface $S$ and boundary path $P$.
\[-\frac{\partial \Phi_B}{\partial dt} = - \int_S\frac{\partial \vec{B}}{\partial t}\cdot d\vec{S} - \oint_P(\vec{v}\times \vec{B})\cdot d\vec{P}\]
**Law 5.1.5 ** The **expanded Faraday's law of induction** states that transformer electromotive force is equal to the time derivative of a slowly varying transformer magnetic flux.
\[\oint\vec{E}\cdot d\vec{\ell} = - \int_S\frac{\partial \vec{B}}{\partial t}\cdot d\vec{S}\]
**Definition 5.1.6 ** The **displacement current density** $\vec{J}_D$ is the effective current density of a changing electric field.
\[\vec{J}_D = \varepsilon_0\frac{\partial \vec{E}}{\partial t}\]
**Result 5.1.7 ** The **magnetic field with displacement current** is the result of Stokes theorem to Maxwell's equations and displacement current density for slowly varying fields.
\[\oint\vec{B}\cdot d\vec{\ell} = \mu_0 \int_S \left(\vec{J} + \vec{J}_D\right)\cdot d\vec{S}\]
\[\oint\vec{B}\cdot d\vec{\ell} =\mu_0 \int_S \vec{J} \cdot d\vec{S} + \mu_0\varepsilon_0 \int_S \frac{\partial \vec{E}}{\partial t}\cdot d\vec{S}\]
### 5.2 Retarded Time
**Definition 5.2.1 ** The **retarded time** $t'$ is the time in the past that position $r'$ appears at when observed from position $r$ and time $t\newcommand\abs[1]{\left|#1\right|}$ due to speed of light $c$ delay.
\[t' = t - \frac{\abs{\vec{r}-\vec{r}'}}{c}\]
**Law 5.2.2 ** The **wave equations for electric potential $V$ and magnetic potential $\vec{A}$** describes how the potentials behave with time varying charge density $\rho$ and current density $\vec{J}$.
\[\nabla^2V - \mu_0\varepsilon_0\frac{\partial^2 V}{\partial t^2} = -\frac{\rho}{\varepsilon_0}\]
\[\nabla^2\vec{A}-\mu_0\varepsilon_0\frac{\partial^2 \vec{A}}{\partial t^2} = -\mu_0\vec{J}\]
\[\vec{\nabla}\cdot\vec{A} +\mu_0\varepsilon_0\frac{\partial V}{\partial t} = 0\]
**Result 5.2.3 ** A Time dependent **[Green's function](https://kaedon.net/l/^1mfe) for the [Laplace operator](https://kaedon.net/l/^59d9)** $G(\vec{r},\vec{r}',t,t')$ is the following function. $\newcommand\abs[1]{\left|#1\right|}$
\[G(\vec{r},\vec{r}',t,t') = \frac{\delta\left(t' - \left[ t - \frac{\abs{\vec{r}-\vec{r}'}}{c} \right]\right)}{\abs{\vec{r}-\vec{r}'}}\]
**Result 5.2.4 ** The **electric potential of a time dependent charge density** can be obtained by direct integration.$\newcommand\abs[1]{\left|#1\right|}$
\[V(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int{ \frac{\rho(\vec{r}',t')}{\abs{\vec{r}-\vec{r}'}} d^3r'}\]
\[V(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int{ \frac{\rho(\vec{r}',t - \frac{\abs{\vec{r}-\vec{r}'}}{c})}{\abs{\vec{r}-\vec{r}'}} d^3r'}\]
### 5.3 Jefimenko's Equations
**Definition 5.3.1 ** **Jefimenko's equations** are a series of integrals that can be used to evaluate the exact electric and magnetic field produced by a time varying charge density $\rho(\vec{r},t)$ and current density $\vec{J}(\vec{r},t)$.
**Result 5.3.2 ** **Jefimenko's equation for electric fields** describes the exact electric field $\vec{E}(\vec{r},t)$ produced by a time varying charge density $\rho(\vec{r},t)$ and current density $\vec{J}(\vec{r},t)$ where $t'$ is the [retarded time](https://kaedon.net/l/^ahc1#zfmr).
\[\vec{E}(\vec{r},t) = \vec{E}_{Coulomb}(\vec{r},t) + \vec{E}_{Charge}(\vec{r},t)+\vec{E}_{Current}(\vec{r},t)\newcommand\abs[1]{\left|#1\right|}\]
\[\vec{E}_{Coulomb}(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int \rho(\vec{r}',t')\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
\[\vec{E}_{Charge}(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int\left[ \frac{1}{c}\frac{\partial \rho(\vec{r}',t')}{\partial t'} \right] \frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^2}d^3r'\]
\[\vec{E}_{Current}(\vec{r},t)=-\frac{1}{4\pi\varepsilon_0}\int\left[\frac{1}{c^2}\frac{\partial \vec{J}(\vec{r}',t')}{\partial t'}\right]\frac{1}{\abs{\vec{r}-\vec{r}'}}d^3r'\]
**Result 5.3.3 ** **Alternate Jefimenko's equation for electric fields** describes the exact electric field $\vec{E}(\vec{r},t)$ produced by a time varying charge density $\rho(\vec{r},t)$ and current density $\vec{J}(\vec{r},t)$. When $\nabla\cdot\vec{J} = 0 $, $\vec{E}_{Currrent1} = 0$ where $t'$ is the [retarded time](https://kaedon.net/l/^ahc1#zfmr).
\[\vec{E}(\vec{r},t) = \vec{E}_{Coulomb}(\vec{r},t)+\vec{E}_{Current1}(\vec{r},t)+\vec{E}_{Current2}(\vec{r},t)\newcommand\abs[1]{\left|#1\right|}\]
\[\vec{E}_{Coulomb}(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int \rho(\vec{r}',t')\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
\[\vec{E}_{Current1}(\vec{r},t)=\frac{1}{4\pi\varepsilon_0c}\int\frac{\left[\vec{J}(\vec{r}',t')\cdot(\vec{r}-\vec{r}')\right](\vec{r}-\vec{r}')+\left[\vec{J}(\vec{r}',t')\times(\vec{r}-\vec{r}')\right]\times(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^4}d^3r'\]
\[\vec{E}_{Current2}(\vec{r},t)=\frac{1}{4\pi\varepsilon_0c^2}\int\frac{\left[\frac{\partial \vec{J}(\vec{r}',t')}{\partial t'}\times(\vec{r}-\vec{r}')\right]\times(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
**Result 5.3.4 ** **Jefimenko's equation for magnetic fields** describes the exact magnetic field $\vec{B}(\vec{r},t)$ produced by a time varying charge density $\rho(\vec{r},t)$ and current density $\vec{J}(\vec{r},t)$ where $t'$ is the [retarded time](https://kaedon.net/l/^ahc1#zfmr).
\[\vec{B}(\vec{r},t) = \vec{B}_{BiotSavart}(\vec{r},t) + \vec{B}_{Current}(\vec{r},t)\newcommand\abs[1]{\left|#1\right|}\]
\[\vec{B}_{BiotSavart}(\vec{r},t) = \frac{\mu_0}{4\pi}\int\vec{J}(\vec{r}',t')\times\left[\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}\right]d^3r'\]
\[\vec{B}_{Current}(\vec{r},t) = \frac{\mu_0}{4\pi}\int\left[ \frac{1}{c} \frac{\partial \vec{J}(\vec{r}',t')}{\partial t'}\right]\times\left[\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^2}\right]d^3r'\]
**Result 5.3.5 ** The **quasistatic expanded Jefimenko's equation** is an expansion of Jefimenko's equations that approximates the electric field $\vec{E}(\vec{r},t)$ and magnetic field $\vec{B}(\vec{r},t)$ produced by a time varying charge density $\rho(\vec{r},t)$ and current density $\vec{J}(\vec{r},t)$ where $t'$ is the [retarded time](https://kaedon.net/l/^ahc1#zfmr).$\newcommand\abs[1]{\left|#1\right|}$
\[\vec{E}(\vec{r},t) = \frac{1}{4\pi\varepsilon_0}\int\left(\rho(\vec{r}',t) - \frac{\abs{\vec{r}-\vec{r}'}^2}{2c^2}\frac{\partial^2\rho(\vec{r}',t)}{\partial t^2} + \cdots\right)\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
\[+\frac{\mu_0}{4\pi}\int\frac{\partial \vec{J}(\vec{r}',t)}{\partial t}\frac{1}{\abs{\vec{r}-\vec{r}'}}+\cdots d^3r'\]
\[\vec{B}(\vec{r},t) = \frac{\mu_0}{4\pi}\int\left[\vec{J}(\vec{r}',t)-\frac{\abs{\vec{r}-\vec{r}'}^2}{2c^2}\frac{\partial^2\vec{J}(\vec{r}',t)}{\partial t^2}\right]\times\frac{(\vec{r}-\vec{r}')}{\abs{\vec{r}-\vec{r}'}^3}d^3r'\]
### 5.4 Electromagnetic Energy and Momentum
**Definition 5.4.1 ** The **electromagnetic energy density** $u$ is the energy density of the electromagnetic fields at a particular point defined in terms of the electric field $\vec{E}$, the electric displacement field $\vec{D}$, the magnetic field $\vec{B}$ and the magnetic field strength $\vec{H}$.
\[u = \frac{\vec{E}\cdot \vec{D} + \vec{B}\cdot\vec{H}}{2}\]
**Result 5.4.2 ** In a **electromagnetic energy density in a vacuum** $u$ can be written in terms of the electric field $\vec{E}$ and magnetic field $\vec{B}$.
\[u = \frac{\varepsilon_0\vec{E}\cdot\vec{E} + \vec{B}\cdot\vec{B}/\mu_0}{2}\]
**Definition 5.4.3 ** The **Poynting vector** $\vec{S}$ is the energy flux (energy per unit area per unit time) of electromagnetic fields at a particular point defined in terms of the electric field $\vec{E}$ and magnetic field strength $\vec{H}$.
\[\vec{S} = \vec{E}\times\vec{H}\]
**Result 5.4.4 ** The **Poynting vector in a vacuum** $\vec{S}$ can be written in terms of the electric field $\vec{E}$ and magnetic field $\vec{B}$.
\[\vec{S} = \frac{\vec{E}\times\vec{B}}{\mu_0}\]
**Law 5.4.5 ** The **electromagnetic conservation of energy law** states that energy is conserved by electromagnetic fields.
\[\frac{\partial u}{\partial t} + \nabla\cdot\vec{S} = -\vec{J}\cdot\vec{E}\]
\[\vec{J}\cdot\vec{E} + \frac{\partial u}{\partial t} = -\nabla\cdot\vec{S}\]
**Definition 5.4.6 ** The **electromagnetic momentum density** $\vec{g}$ is the momentum density of the electromagnetic fields at a particular point defined in terms of the electric field $\vec{E}$ and magnetic field strength $\vec{H}$.
\[\vec{g} = \frac{\vec{E}\times\vec{H}}{c^2} = \frac{\vec{S}}{c^2}\]
**Definition 5.4.7 ** The **Maxwell stress tensor** or **momentum flux tensor** $T_{ij}$ is the 3 by 3 matrix describing the momentum flux (momentum per unit area per unit time) that is the change in each component of momentum in each direction defined by the the electric field $\vec{E}$ and magnetic field $\vec{B}$ in a vacuum.
\[T_{ij} = \varepsilon_0\left[ E_iE_j + c^2 B_iB_j - \frac{1}{2}\left(\vec{E}\cdot\vec{E} + c^2\vec{B}\cdot\vec{B}\right)\delta_{i,j}\right]\]
**Law 5.4.8 ** The **electromagnetic conservation of momentum law** states that momentum is conserved by electromagnetic fields.
\[\frac{d\vec{p}_{mech}}{dt} = q(\vec{E} + \vec{v}\times\vec{B})\]
\[\vec{p}_{field} = \varepsilon_0\int_V\vec{E}\times\vec{B} dV = \int_V \vec{g} dV\]
\[\left[ \frac{d\vec{p}_{mech}}{dt} + \frac{d \vec{p}_{field}}{dt}\right]\cdot \hat{k} = \oint_S\sum_jT_{k,j}n_j dS\]
where $k\in\{x,y,z\}$ and $\hat{n}$ is the vector pointing out of the surface $S$ that bounds the volume $V$.
**Definition 5.4.9 ** The **Maxwell stress 4-tensor** $\Omega^{\alpha,\beta}$ is the 4-tensor that can be used to describe the energy and momentum of electromagnetic fields in different reference frames.
\[\Omega = \begin{pmatrix} u & c\vec{g} \\ c\vec{g} & -T \end{pmatrix} =
\begin{pmatrix}
u & cg_x & cg_y & cg_z\\
cg_x & -T_{xx} & -T_{xy} & T_{xz}\\
cg_y & -T_{yx} & - T_{yy} & - T_{yz}\\
cg_z & -T_{zx} & -T_{zy} & -T_{zz}
\end{pmatrix}\]
**Result 5.4.10 ** The **Lorentz boost of a 4-tensor** can be computed by applying the [Lorentz boost matrix](https://kaedon.net/l/^ahc1#059k) $\Lambda(\vec\beta)$ to a 4-tensor $T$.
\[T' = \Lambda(\vec{\beta})T\Lambda^\top\]
### 5.5 Multipole Radiation
**Result 5.5.1 ** The **power radiated from a rotating multipole** $P_{radiated}$ can be written in terms of the oscillation frequency and the multipole expansion $\vec{p},\vec{m},Q_{jk},\cdots\newcommand\abs[1]{\left|#1\right|}$ of the charge distribution.
\[P_{radiated} = \frac{Z_0\omega^4}{12\pi c^4}\left[ \abs{\vec{p}}^2 + \abs{\frac{\vec{m}}{c}}^2 + \frac{\omega^2}{120 c^2}\sum_{jk}\abs{Q_{jk}}^2 + \cdots \right]\]
**Result 5.5.2 ** The **solid angle distribution of multipole radiation** describes the angular distribution of the power radiated by a rotating multipole.
\[\frac{\partial P}{\partial \Omega} \propto \omega^4 q^2 (r')^2\sin^2(\theta)\]
\[\frac{\partial P}{\partial \Omega} \propto \omega^4\left[ \frac{I}{c}(r') \right]^2(r')^2\sin^2(\theta)\]
\[\frac{\partial P}{\partial \Omega} \propto \omega^4\left[ \omega\frac{q}{c}(r') \right]^2(r')^2\sin^2(\theta)\cos^2(\theta)\]
**Definition 5.5.3 ** The **vector spherical harmonics** $\vec{X}_{\ell,m}(\theta,\phi)$ are generalizations of spherical harmonics for vectors fields.
\[\vec{X}_{\ell,m}(\theta,\phi) = \frac{-i(\vec{r}\times\nabla)Y_{\ell,m(\theta,\phi)}}{\sqrt{\ell(\ell + 1)}}\]
**Result 5.5.4 ** The **general electromagnetic multipole radiation** generated by electric multiple moments $a_M^{\ell,m}$ and magnetic multipole moments $a_E^{\ell,m}$ oscillating at frequency $\omega$ can be written in terms of [Vector Spherical Harmonics](https://kaedon.net/l/^ahc1#pa5a) $\vec{X}_{\ell,m}(\theta,\phi)$.
\[\vec{E} = \text{Real}\left( \sqrt{\frac{\mu_0}{\varepsilon_0}} \sum_{\ell,m}\left[ a_E^{\ell,m}\nabla\times\left( \frac{i}{k}f_\ell(kr)\vec{X}_{\ell,m} \right) + a_M^{\ell,m}g_\ell(kr) \vec{X}_{\ell,m} \right] e^{-i\omega t} \right)\]
\[\vec{B} = \text{Real}\left( \mu_0\sum_{\ell,m}\left[ -a_E^{\ell,m}\nabla\times\left( \frac{i}{k}g_\ell(kr)\vec{X}_{\ell,m} \right) + a_M^{\ell,m}f_\ell(kr) \vec{X}_{\ell,m} \right] e^{-i\omega t} \right)\]
\[f_\ell(kr) = A_\ell^{(1)}H_\ell^{(1)}(kr) + A_\ell^{(2)}H_\ell^{(2)}(kr)\]
\[g_\ell(kr) = B_\ell^{(1)}H_\ell^{(1)}(kr) + B_\ell^{(2)}H_\ell^{(2)}(kr)\]
\[k = \frac{\omega}{c}\]
where $A_\ell^{(1)}, A_{\ell}^{(2)}, B_\ell^{(1)}, B_\ell^{(2)}$ are coefficients determined by boundary conditions and $H_\ell^{(1)}, H_\ell^{(2)}$ are [Hankel functions](https://kaedon.net/l/^ahc1#emjk).
**Result 5.5.5 ** The **electric multipole moment $a_E^{\ell,m}$ due to an oscillating charge density** $\rho$ oscillating at angular frequency $\omega$ (wavenumber $k=\omega/c$) can be written as integrals of [spherical harmonics](https://kaedon.net/l/^ahc1#hae2) $Y_{\ell,m}^*$ and [Bessel functions](https://kaedon.net/l/^ahc1#et2j) $J_{\ell + 1/2}$. The multipole moment can be approximated when the wavelength is much greater that the size of the source.
\[a_E^{\ell,m} = \frac{k^2}{i\sqrt{\ell(\ell + 1)}} \int Y_{\ell,m}^*(\theta,\phi)\left[ c \rho(\vec{r}) \sqrt{\frac{\pi}{2kr}}\frac{\partial \left(r J_{\ell + 1/2}(kr)\right)}{\partial r}\right] d^3r\]
\[a_E^{\ell,m}\approx\frac{ck^{\ell+2}}{i(2\ell + 1)!!}\sqrt{\frac{\ell + 1}{\ell}}\int r^\ell Y_{\ell,m}^*(\theta,\phi)\rho(\vec{r})d^3r\]
**Result 5.5.6 ** The **multipole moment $a_E^{\ell,m},a_M^{\ell,m}$ due to an oscillating current density** $\vec{J}$ oscillating at angular frequency $\omega$ (wavenumber $k=\omega/c$) can be written as integrals of [spherical harmonics](https://kaedon.net/l/^ahc1#hae2) $Y_{\ell,m}^*$ and [Bessel functions](https://kaedon.net/l/^ahc1#et2j) $J_{\ell + 1/2}$. The multipole moment can be approximated when the wavelength is much greater that the size of the source.
\[a_E^{\ell,m} = \frac{k^2}{i\sqrt{\ell(\ell + 1)}}\int Y_{\ell,m}^*(\theta,\phi)\left[ ik\vec{r}\cdot\vec{J}(\vec{r})\sqrt{\frac{\pi}{2kr}}J_{\ell + 1/2}(kr) \right] d^3r\]
\[a_E^{\ell,m} \approx 0\]
\[a_M^{\ell,m} = \frac{k^2}{i\sqrt{\ell(\ell + 1)}}\int Y_{\ell,m}^*(\theta,\phi)\left[ \nabla \cdot \left( \vec{r}\times\vec{J}(\vec{r})\right) \sqrt{\frac{\pi}{2kr}}J_{\ell + 1/2}(kr)\right] d^3r\]
\[a_M^{\ell,m}\approx \frac{ik^{\ell+2}}{(2\ell + 1)!!}\sqrt{\frac{\ell}{\ell + 1}}\int (r)^\ell Y_{\ell,m}^*(\theta,\phi)\nabla\cdot\left( \vec{J}\times\vec{r} \right) d^3r\]
**Result 5.5.7 ** The **multipole moment $a_E^{\ell,m},a_M^{\ell,m}$ due to an oscillating magnetization** $\vec{M}$ oscillating at angular frequency $\omega$ (wavenumber $k=\omega/c$) can be written as integrals of [spherical harmonics](https://kaedon.net/l/^ahc1#hae2) $Y_{\ell,m}^*$ and [Bessel functions](https://kaedon.net/l/^ahc1#et2j) $J_{\ell + 1/2}$. The multipole moment can be approximated when the wavelength is much greater that the size of the source.
\[a_E^{\ell,m} = \frac{k^2}{i\sqrt{\ell(\ell + 1)}} \int Y_{\ell,m}^*(\theta,\phi)\left[ -ik\nabla\cdot\left( \vec{r}\times\vec{M}(\vec{r}) \right) \sqrt{\frac{\pi}{2kr}}J_{\ell+1/2}(kr) \right] d^3r\]
\[a_E^{\ell,m} \approx -\frac{k^{\ell + 2}}{(2\ell + 1)!!}\sqrt{\frac{1}{\ell(\ell + 1)}}\int(r)^\ell Y_{\ell,m}^*(\theta,\phi)\left[ \nabla\cdot(\vec{r}\times\vec{M}(\vec{r})) \right] d^3r\]
\[a_M^{\ell,m} = \frac{k^2}{i\sqrt{\ell(\ell+1)}}\int Y_{\ell,m}^*(\theta,\phi)\left[ -k^2\left(\vec{r}\cdot\vec{M}(\vec{r})\right)\sqrt{\frac{\pi}{2kr}}J_{\ell + 1/2}(kr) \right]d^3r\]
\[a_M^{\ell,m}\approx -\frac{ik^{\ell+2}}{(2\ell+1)!!}\sqrt{\frac{\ell + 1}{\ell}}\int (r)^\ell Y_{\ell,m}^*(\theta,\phi)\left( \nabla\cdot\vec{M}(\vec{r}) \right)d^3r\]
### 5.6 Moving Charges
**Result 5.6.1 ** The **electromagnetic fields from an accelerating point charge** at position $\vec{r}_{charge}$ observed at position $\vec{r}_{obs}$ can be written as the following two terms. The first term is the "velocity field" which dominates in the quasi-static regime and the second term is the "acceleration field" which dominates in the radiation regime.
\[\vec{E} = \frac{q}{4\pi\varepsilon_0}\left[\frac{\beta}{\gamma^2 R^2}\cdot\frac{\hat{R}/\beta - \hat{\beta}}{\left(1-\vec{\beta}\cdot\hat{R}\right)^3}\right]_{ret} + \frac{q}{4\pi\varepsilon_0}\left[\frac{\beta\dot{\beta}}{cR}\cdot\frac{\hat{R}\times\left( \left(\hat{R}/\beta - \hat{\beta}\right)\times\dot{\hat{\beta}} \right)}{\left(1-\vec{\beta}\cdot\hat{R}\right)^3}\right]_{ret}\]
\[c\vec{B} = \left[\hat{R}\times\vec{E}\right]_{ret}\]
\[\vec{R} = \vec{r}_{obs}-\vec{r}_{charge}\]
**Definition 5.6.2 ** The **Larmor power** $P_{Larmor}$ is the power radiated by an accelerating particle with acceleration $\dot{\beta}$ in the non-relativistic limit.
\[P_{Larmor} = \frac{q^2 \dot\beta^2}{6\pi\varepsilon_0 c}\]
**Result 5.6.3 ** The **relativistic Larmor formula** describes the power radiated $P_{rad}\newcommand\abs[1]{\left|#1\right|}$ by a relativistic accelerating particle.
\[P_{rad} = \gamma^6\left[1-\abs{\hat{\beta}\times\hat{\dot{\beta}}}^2\beta^2\right]P_{Larmor} = \gamma^6\left[1-\abs{\hat{\beta}\times\hat{\dot{\beta}}}^2\beta^2\right] \frac{q^2 \dot\beta^2}{6\pi\varepsilon_0 c}\]
\[\frac{dP_{rad}}{d\Omega} = \frac{q^2}{16\pi^2\varepsilon_0c}\frac{\abs{\hat{R}\times\left(\left(\hat{R}-\vec{\beta}\right)\times\dot{\vec{\beta}}\right)}^2}{\left(1-\hat{R}\cdot\vec{\beta}\right)^5}\]
\[\vec{R} = \vec{r}_{obs}-\vec{r}_{charge}\]
## 6 Appendix
### 6.1 References
[^32ca]
[^32ca]: Richard S. Davis; Determining the value of the fine-structure constant from a current balance: Getting acquainted with some upcoming changes to the SI. Am. J. Phys. 1 May 2017; 85 (5): 364–368. https://doi.org/10.1119/1.4976701